Over the years the topic of the simulation of the properties of swords has come up a number of times. I happen to have worked on that a few years ago, and this post desribes the results I have obtained.
I have built a small Scilab program to simulate blade harmonics and dynamic properties (pivot points, center of gravity, mass), taking as inputs parameters from the materials (density, elasticity) and geometry (lengths and cross-sections). I chose a simple model for the sword, in fact one of the simplest models for slender, flexible beams (the name of the model is Euler-Bernoulli), that allows a varying cross-section along the length of the beam. The program solves the equation from the model using a 1D finite elements approach. In addition to rigid-body dynamic properties (mass, center of gravity, pivot points), it finds the modes of vibration, assuming that the sword is not constrained by anything. That is an appropriate model to simulate the very relaxed grip that is assumed when looking for vibration nodes.
Being satisfied with the behavior on basic test cases (uniform bar, simple taper, and so on), I decided to go for something a bit less obvious and tried to simulate a real sword of mine: my Angus Trim type XI. To be honest, I was expecting a more or less spectacular failure.
I measured as precisely as I could cross sections across the blade, as well as the pommel and cross-guard. I didn’t want to go through the trouble of unmounting the sword so I made some reasonable guess for the tang based on what I remembered. I completely neglected the grip.
I ended up with 7 parts for the sword, over which I assumed the variation were linear, that I further subdivided in elements roughly according to their length:
- pommel (1 element)
- tang (5 elements)
- cross (1 element)
- upper part of the blade (30 elements)
- middle part of the blade (10 elements), the fuller stops here
- upper part of the blade (5 elements), not fullered
- tip (1 element)
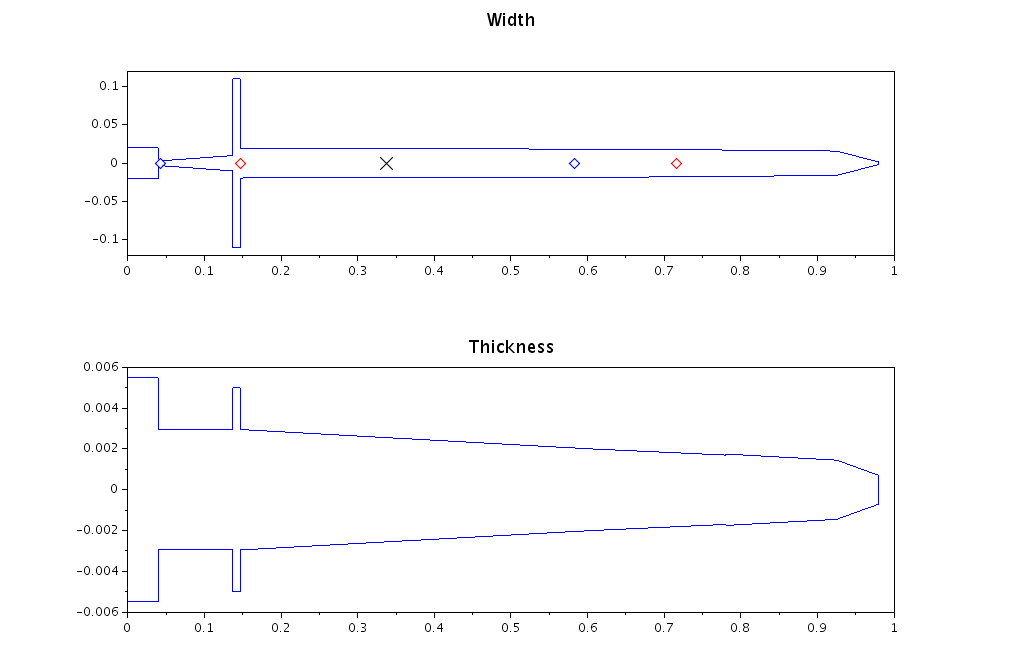
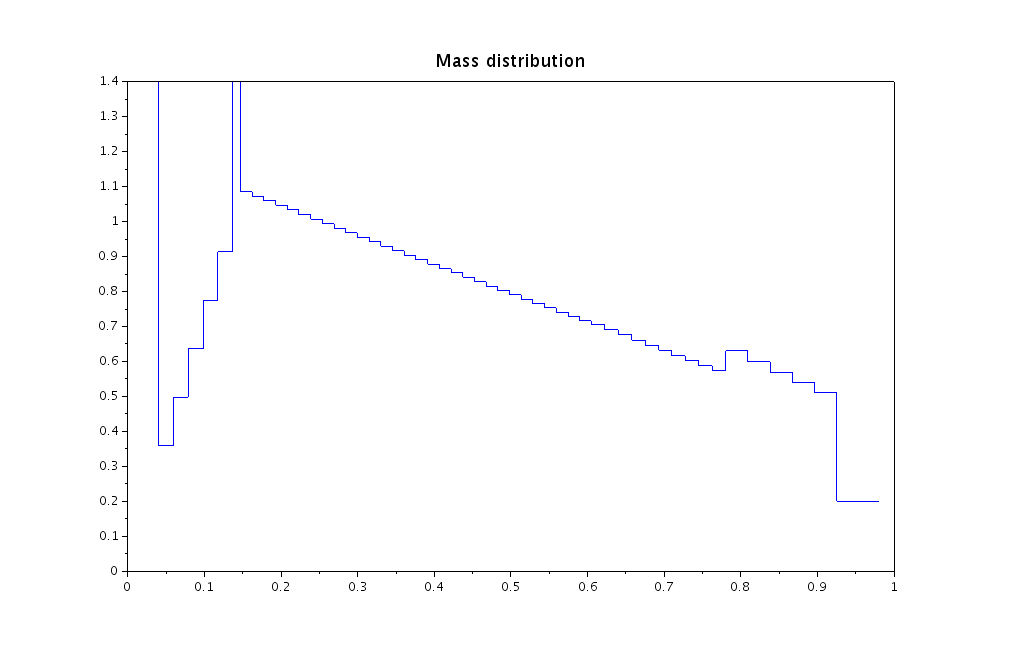
I entered all this into my program, along with average values of density and Young modulus for steel, aft and forward positions on the grip (to compute aft and forward pivot points). I was then able to compute an approximate mass distribution, and rigid body dynamic properties:
The center of gravity is marked here with a black cross. The aft pivot point pair is represented by blue diamonds, the forward pivot point pair by red ones. The dynamic properties are found with a precision better than half a centimeter (far better than I can measure anyway). I just tweaked slightly the pommel shape to adjust even better (when I say slightly, it’s 1mm in thickness…). And that is with all the approximation made, and a very rough model of the fuller.
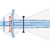
My program can compute modes of vibration for the sword, which of course gives the nodes in particular.
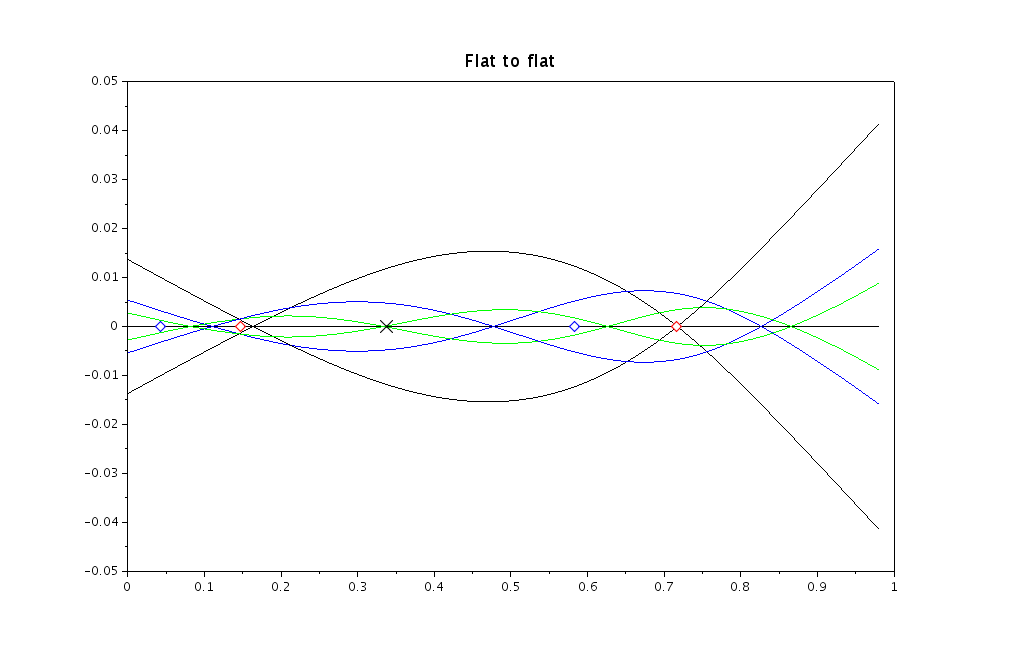
The modes of vibration, computed here in the flat to flat plane, which is the one we are able to observe.
The straight black line is the axis of the undisturbed sword. The tip of the sword is to the right. The curves represent the modes of vibration. The first mode, that is used to determine the blade node and hilt node, is in black. The curves are scaled according to the energy of the sword when it vibrates in that mode: the higher the mode, the less ample the vibration becomes. I plotted only the three first modes to keep the figure clear. For each mode, I made two symmetric curves, that indicate the deformation of the sword bending one way, then the other. The harmonic nodes are precisely computed, from what I can see. The blade node is exactly right, the hilt node is a bit more difficult to measure, but seems to be spot-on as well.
I had to adjust the density slightly to account for the mass of the sword. My first simulation was giving a mass of 950g, while my sword weights 1009g. This uniform change does not moves the nodes or pivot points at all (this is a mathematical property of the model I use). It might indicate that my measurements were not perfectly accurate, which is likely given the approximation made especially on the cross-section shape.
Interesting virtual experiments can be done with this program. For example, the pommel and cross can be virtually removed. Here is how the properties change:
I remain convinced that the interest of such simulation is limited, because the perceptible results (dynamics, nodes of the first mode of vibration) are easily measured on swords. However, it shows what is sufficient to obtain the observed effects. It also disproves a relatively widespread idea on this matter, that it should take an army of scientists and a cluster of supercomputers to accurately model and simulate the behavior of a sword because they are somehow “infinitely complex”. I must stress that I did all that using well-known mathematical methods and the simplest models, implemented in the most direct fashion, and that the core of the computation runs in about 0.1 second on my laptop (far less than what it spends plotting the results, in fact. The total is about 1s…). It proves me wrong as well, because before doing this I used to think that the number of cross sections that should be measured would have to be far greater…
Most modern 3D CAD programs would make these computations easier, and probably more accurate and stable as well. I have mainly done this code to gain some experience in finite element modeling on a topic I enjoy. I’m not really expecting this to be robust or easy to use. Find the code in this zip file! Just unzip it, launch Scilab, set the working directory to the folder containing swordSimulFunc.sce, edit swordSimul.sce, or even create a new file as needed and execute it. I do not have time to support or document this much more, so you will be pretty much on your own if you want to dig deeper. If you do end up with something valuable, please share!


Thank you for your post! I have a couple questions about this and the sword dynamics calculator in general. First, I have an antique Chinese blade that is rather thick and stiff and vibration nodes are not easily visible when I tap the sword. I have a feeling that the model you have outlined here would be helpful in determining the vibration nodes of such a blade, but does this formula still work on forge-welded (laminated) swords? Furthermore, is it actually important to calculate the vibration nodes on something like a katana? Many differential hardened blades can be very stiff and I am not sure that the vibration nodes have the same impact on cutting that they would on a more “springy” blade, but I wanted to know your thoughts on the matter. Many thanks!
Hello!
The model outlined here can simulate things, but really if you cannot observe the nodes in any way they are probably not that significant in your particular case. The simulation is very dependent on precise measurements of cross-sections, and frankly they are quite painful to make. So much so that I never bothered doing another practical application 🙂 I’m mainly using this simulator to test hypothesis on where the nodes should be for different, theoretical blade profiles.
This being said I’ve been able to spot the node even on very stiff objects, for example wooden swords, iron bars, thick steel blades. If the sword is so stiff that it does not visually vibrate, the node can be sometimes be found by tapping at different locations, until the one that causes the shortest, highest pitch vibration is reached. In my experience, the main constraint is rather how tight the assembly is. Any gap or play in the mounts is going to dampen the vibrations, and too much dampening is what makes it impossible to view or feel the vibrations. I have not had the opportunity to study many forge welded blades, but the ones I have seen still had perceptible nodes, so I don’t think the blade material itself will change the behaviour significantly in this regard. But more experiments are always warranted!
The question of how important the nodes really are for cutting behaviour is a difficult one, and it is largely open. On flexible blades there are two main effects of hitting outside the blade node:
blade flex will mess up edge alignment
the maximum force exerted on target will be lower – the impact is cushioned so to speak
Peter Johnsson has pointed out that the nodes are points of stiffness in a sense. When forces are applied to either nodes the sword reacts as if it was stiffer. On wooden sticks the second effect can still be perceived. I would therefore expect it to show also on stiff blades, but we’d need to investigate to which degree it really matters. What target you’re striking also matters here.
Thanks for your interest!