The blog SwordSTEM has published an article about vibrations on swords:

Analysis of the Vibrational Characteristics of a Training Longsword

It is nice to see people tackling the quantitative approach of these aspects. Certainly sword science in general could use more data, and a study of the details of swords vibratory behaviour has a lot of potential depth and ramifications. However there are a number of problems in the article here and its conclusions. Some of them would only be apparent to people familiar with swords and I feel they need to be restated here.

Generalities on swords vibrations

The article quickly skims over most of the existing theory of vibrations in general and sword vibrations in particular, so I will try to provide some sort of summary here.

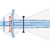
Most European swords are flexible to a degree, and elastic: they are treated to be able to bend and return to true. Their assembly is also generally tight. This makes them susceptible to vibrations. The most commonly observed vibratory effect is the presence of two vibration nodes which seem not to vibrate, one on the blade, one on the hilt or near it. When the sword is hit on its flat, it vibrates and the nodes become visually apparent. When it is hit at the nodes, the amplitude of the vibrations is much smaller. The nodes have been therefore associated to the possibility to reduce vibrations, both because they do not vibrate and because impacts on them cause minimal vibrations.

Most people’s understanding of sword vibrations stop there, but in order to productively discuss the article we need to go a little deeper into what vibration modes are.

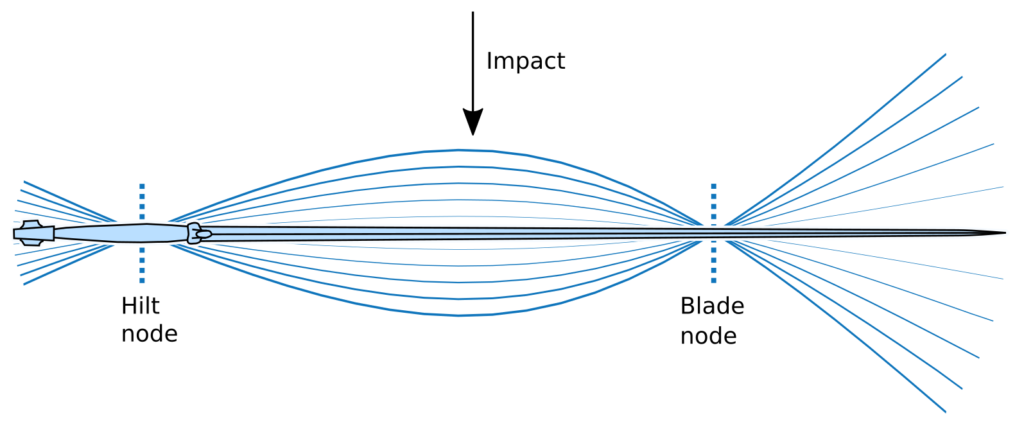
In general all points of a flexible object can move independently from one another, although this is of course constrained by the elasticity of the material. A mode of vibration is a specific pattern of motion where all points of the object vibrate together, with the same frequency and phase, but with different amplitudes. For objects such as European swords, which are flexible and elastic with only a little damping, there is – in theory – an infinity of discrete vibration modes, each associated to a vibration frequency and a specific mode shape taken by the object as it deforms. The modes can be ordered from the lowest frequency (slowest vibration) to the highest.

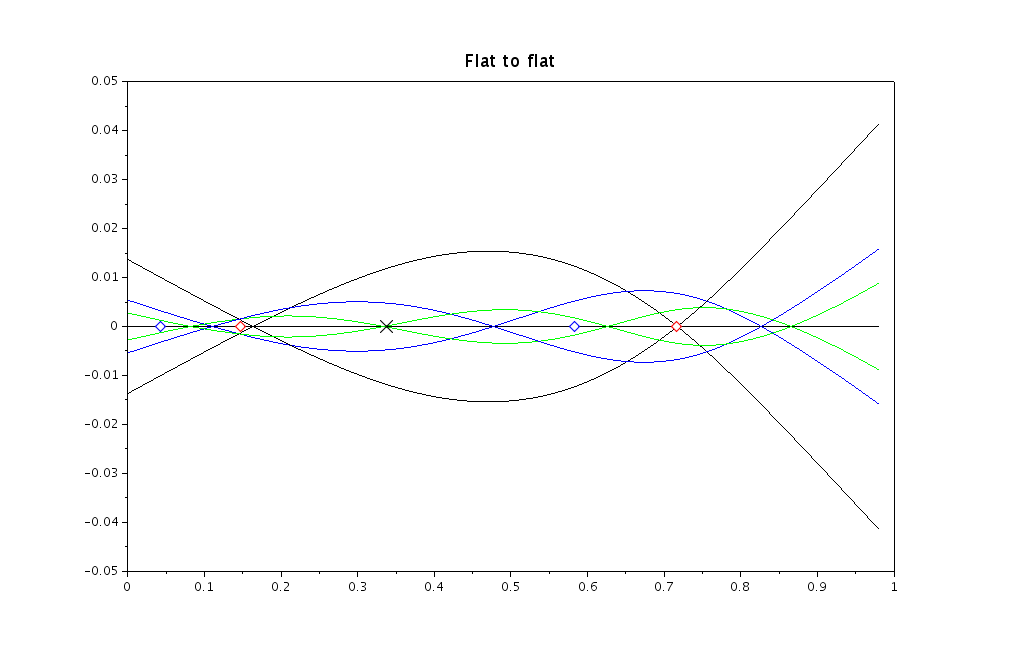
Modes of vibration, by definition, do not involve any rigid body motion. The center of gravity, for example, remains unchanged. This means that the axis of the resting position intersect all of the mode shapes, as shown in the above figure. These points of intersection which have no motion at all in a given mode are called nodes of vibration. The study of modes of vibration in an object is called modal analysis.

The most visible mode of vibration is the first mode, sometimes called primary mode. It is the mode that has the biggest amplitude for a given energy, and whose vibrations are least affected by damping. This is the one we observe in the simple measurement above. On a few swords, by hitting precisely at the blade node, I have also been able to observe the second mode of vibration as well, which has three nodes.

Vibration modes strongly depend on the boundary conditions imposed to the object: stick the point of a sword in the ground and suddenly different modes appear. In the measurement method above one seeks to get as close as possible to free vibrations by using a very light grip, or gripping close to the hilt node.

A final point to understand is that nodes are not really areas where no movement at all ever occurs in any experimental condition achieved by impacts at a variety of points on the sword. Impact at any point stimulates all the modes, not just the first one, as well as the rigid body dynamic response of course. This is a well-known property in modal analysis. However, the first mode of vibration is the longest lasting with the biggest amplitude, and therefore quickly becomes the only perceptible vibration once it has been excited. Impacts at the nodes do not excite the first mode, leaving us with mostly the rigid body response and quickly dampened higher modes, which is why people aim to hit with the node to reduce vibrations. Anyway, by their very definition nodes cannot vary through time along the length, although the combination of several modes of vibration might have that effect of creating temporary fixed points at different places as the blade vibrates.

A number of practical ways to find the nodes could probably be devised if you don’t trust your hands and eyes, the two main varieties being:

1. impose vibrations of varying frequencies to the sword, and detect resonance
2. make an impact on the sword and precisely measure the acceleration at many spots of the blade, then basically make Fourier analysis to get the modes of vibration.

If I had to do it I would pick 2. as it could also give access to the nodes, picking the place where the vibrations are of the smallest amplitude. But really, on sword-like objects, the blade node at least is generally apparent to the eye.

Detailed review of the article

The root question of the article is a very pertinent one. The whole previous analysis, as well as the practical measurement described above, seeks the nodes that appear under very specific ‘free’ boundary conditions. In use swords are obviously held in our hands and therefore not free. The aim of the article seems to be to study the effect of the grip on the modes of vibration and node location.

Model

The sword model is nice, perhaps even too detailed on the hilt. But the boundary conditions used are entirely unrealistic: no swordsman hands are going to be able to stop the vibrations of a sword. The frequency is just too high for our flesh and muscle to entirely counter (although they do dampen them), and this can be readily observed when looking at what happens to your hands when the blade vibrates. So nobody ever strikes a clamped sword like this. The primary mode of vibration of a clamped object is to just vibrate side to side from the fixed point. There would be no noticeable node. This is what the more accurate Solidworks simulation shows, but even accurate simulation cannot give realistic output if the inputs are flawed.

Solution

The Solution part makes the additional hypothesis that the blade is uniform along its length, which is absolutely not true for swords intended for any practical use. Distal and profile taper have a strong impact on any vibration property. Thus the analytical solution presented has little relevance except in as much as it gives some order of magnitude for the vibrations to be observed; sadly as mentioned in the previous paragraph the boundary conditions do not apply to any practical situation anyway. I have not thoroughly checked the calculations but I suspect there is an error in them as well, because on the displacement graphs you will note the tip never moves, which should not be the case, even under these conditions (and Solidworks confirms this).

Results

Photographic analysis is always going to be hard, and I would prefer if the experimenter checked with his own perception as well. I am pretty sure the person holding the sword could see nodes quite clearly. There are two problems with the photographs here:

• they cannot easily be realigned while correcting for the rigid body motion. You could take the same pictures and realign them in a variety of ways which would show nodes all over the place
• there is no guarantee that the captured image shows the extreme positions of vibrations, which compounds with the first issue

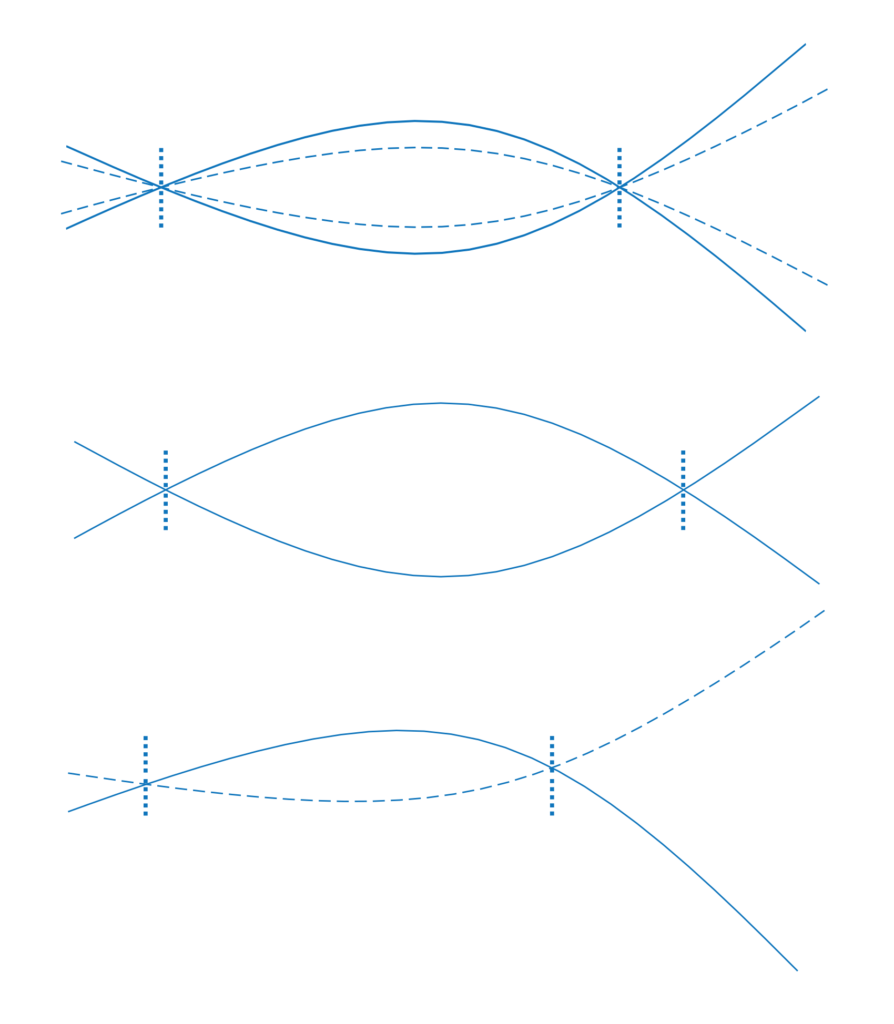
What marks the results as dubious in this section is the fact that the vibration shapes are not symmetrical, while modes of vibration of symmetrical objects always are. Another point to note is that the shape of the flex is pretty different from the simulations of clamped swords, which is a strong indicator that the clamped model is a poor reflection of reality, arguably even worse than the common ‘no hand influence’. That being said, this photographic documentation is the part that comes the closest to the stated goal of studying sword vibrations when they are held, and not as independent objects.

The idea of recording sound to find the modes is interesting, however you would need evidence that the ring we hear when we strike a sword is indeed due to the blade. The first mode of vibration (in a free-free boundary condition) according to simulation is somewhere around the tenth of Hz, which is very low, at the lower range of our hearing. I personally suspect that the ring we hear is rather that of the cross-guard. At least on all my swords, touching the cross stops the ringing immediately, although the blade keeps vibrating. So I think the authors have just measured the quillon first mode of vibration here.

Modification

This section misses a crucial method. It is a well-known effect that changing pommel weight alters the balance but also the vibration behaviour. This is easily tested with a sword that can be disassembled: the bare blade transmits more shock in general, and more vibrations specifically, to the hand. This is actually the primary modification that should be discussed – and figuring how the nodes move upon weight modification is a whole other project!

Some swords vibrate less than others. Japanese swords in particular, according to people who have interacted with them more than I did, tend to be very hard to measure nodes on. I suspect some of it is due to the grip construction which acts as a damping device, but this would need to be investigated further. It might provide a more interesting solution than damping material in gloves, which I suspect would wreck dexterity, and is nowhere to be seen historically.

My take on the issue

It is only fair to share my own point of view on the issue of how the hand interacts with the nodes and influences vibrational behaviour. I will not venture into the complex issue of the magnitude of the effects of vibrations on sword performance in general, but consider just vibrations on their own.

There are two effects that hands can have:

• Changing vibration modes – node position, mode shape, frequency
• Damping vibrations

The first effect is unavoidable as long as you consider that at least some of the hands/arms mass is moving together with the sword. The second effect is generally going to feel bad for the swordsman: some energy is going to be dissipated into the body. If you are trying to stop vibrations after they have appeared, you are going to rely on the second effect. If you want to minimize the apparition of vibrations, you are going to need an understanding of the first effect.

If the hand was gripping just exactly at the hilt node, it would feel no vibration for the primary mode, and would not change the location of the blade node either. It would change the higher modes though, but this is much harder to perceive or feel. If on the top of that you hit with the blade node, very little vibration would occur altogether. This seems to be the idea behind most sword’s design.

Our hands are not points however, and we have two of them on some swords. The primary mode shape is therefore affected. The effect on the second hand on the grip is certainly the biggest, and qualitatively similar to the addition of a pommel: more mass at the very end of the grip. The effect of adding a pommel has been documented by swordsmiths (and can be confirmed by simulation): the hilt node is ‘attracted’ to the added mass, but the blade node remains mostly unchanged, displaced by a few centimeters at most. The mass to be considered is that of the hand, plus some fraction of the forearm and arm. In all likelihood, it is less than a kilogram.

The expected effect of the gripping hand is therefore that the blade node is marginally displaced towards the hilt, and the hilt node slightly moved towards the center of mass of the hands – which would have to be determined and depends on the exact grip used, but inevitably lies between the hands, quite close to where the hilt node already lies.

The only way to achieve a more dramatic effect, akin to the boundary conditions used in the article, would be to involve more of the body mass behind the grip via muscular contraction. Empirically, this seems to mostly dampen the vibrations, rather than fix the grip totally. I have been entirely unable to sustain the sort of cantilever beam vibration that would be expected in this case, however hard I tried. It is well-known that having a death grip on a sword’s handle, or contracted arms and shoulders, is not leading to any good fencing, and forcing the muscles to absorb vibratory energy is perhaps the least of the drawbacks.

More measurements would be warranted of course, but the expected result for me is that nodes are only slightly affected by a proper gripping action, and that therefore the study of the free vibrations of swords is appropriate as it does not need any further assumptions about the grip strength and method.

Conclusion

It seems like the authors got caught up in the technical approach, from many directions, but never stopped to thoroughly cross-check the results or evaluate the precision of the methods they use and the assumptions behind their models. It is valid to question the assumption that the hand has no influence on the nodes, but it needs to be investigated with methods that can actually find nodes in the first place. The conclusion that everything we think we know about nodes is wrong is at best hasty, and quite misleading for the people who do not have the depth of technical and scientific understanding to see the problems with each of the approaches described and how they influence the conclusion.

I do hope the authors stick with this area of study and revisit their work. I will certainly read future articles on this topic with great interest!