When studying the function of swords and other hand-held weapons, a question that inevitably rises is how they perform one of their primary tasks, which is to cause damage to a target. It turns out that this question can be harder to answer scientifically than one would expect. It is possible to come to this problem from several directions; for example how much force can a sword apply in a cut, what is the best place on a sword to hit with, what are the relative influences of mass and speed on the damage done, etc.

The article of Georges Turner gives a good overview of how a sword blow works, but skips important details of what happens during impact, and does not consider the way in which damage is caused. Another recent article goes into more detail, but focuses on an analysis in terms of force that abstracts away any damage model. Yet another article tries to model damage, but the author’s apparent misunderstandings of fundamental physics together with the intent of proving a predetermined conclusion lead him astray (this article has since been removed, which is not a big loss; some discussion of it can be found here). I have therefore decided to confront the problem myself!

This article will remain purely in the theoretical realm. First I will describe how the impact can be modeled and simplified, then consider global balances that will always be true, and finally explore what can exactly happen during the brief time of the collision and how this influences the expression of the damage.

Since I am concerned with the physical and mathematical modelisation of impacts here, inevitably maths are going to be involved. I have tried to keep formulas to a minimum in the main text, and provide demonstrations of the conclusions in this sort of hidden sections:

In order to fully get the main text, some familiarity with physics is still going to be assumed. You have to be aware of Newton’s laws, of the relationships between position, speed, acceleration, force and mass. An understanding of kinetic energy and momentum will be useful.

Problem simplification

A complete study would take into account the full motion, mass distribution and geometry of the weapon, the reaction of the target, and the reaction of the weapon user. This becomes mathematically nightmarish very quickly. In particular, the user’s reaction involves not only the mechanical modelling of the human body, but also of the nervous system, and depends on the training and intent. In order to obtain a system that can be more readily apprehended and manipulated, we have to make some simplifying assumptions.

First we will consider that the contact between the weapon and target remains such that different parts of the weapon in contact with the target do not have different speeds. This allows to simplify the weapon and target into two interacting point masses with some initial relative speeds, along a single axis. This is generally verified either because the target is small relative to the weapon (as in many cuts), or because the motion of the weapon does not create different speeds in different locations (in thrusts for example).

With no loss of generality, we can assume that the target is initially static. For a target moving at a constant speed, we can simply consider the problem in the target’s frame of reference. Although the target’s own motion could have acceleration irrespective of the effect of the impact, it will normally be negligible compared to the speed and duration of the collision.

We will further assume that the user reaction does not meaningfully contribute to target damage. The user appears passively by adding some of its body mass to that of the weapon, but not by actively pushing into the target. This defines the effective mass of the weapon. In a thrust, the whole mass of the sword and a significant fraction of the user’s mass would be involved in the effective mass. In a cut, it is not the same. If the sword alone is considered, only a fraction of its mass resists forces, depending on the location on the edge. This curve is displayed in the Weapon Dynamics Computer. A minor amount of the sword user’s mass could be added to this.

This is a more debatable assumption. It is however corroborated by some sources, such as Colonel Marey:

In the cut, a sword should be considered in the light of a projectile, of which the portion in the neighbourhood of the point has a much greater velocity than the hilt. The hand gives it this impulse, and does not act by pressing the sword on the body to be penetrated at the moment of impact.
Colonel Marey, Memoir on swords etc. (1841, trans. 1860)

If the forces generated on the target are very big, i.e. the target is fairly hard to cut, this will be verified. Indeed, due to leverage, your hand cannot generate a meaningful amount of force on the business end of the weapon. The softer the target, the less true it becomes. To take an extreme case, when you are cutting air it is obviously not true. Two-handed weapons with great leverage, or shorter weapons such as daggers and knives, will also make it easier to apply force directly. Generally speaking, if you are able to cause sizeable damage to the target by just pressing on it with no initial speed, this is not verified.

Note that if a complex target is considered, it is necessary to evaluate its effective mass as well. A target solidly fixed to the ground basically has the effective mass of the Earth…

To sum up and introduce notations, let us consider a target of mass \(m_i\), initially at rest, being hit by a weapon of effective mass \(m_w\) moving at initial speed \(v_0\).

Simplifying the impact problem. Sword user and target are abstracted as two point masses \(m_w\) et \(m_i\), the weapon moves at initial speed \(v_0\).

We will assume that the impact is perfectly inelastic, meaning that the weapon and target eventually acquire the same speed \(v_f\) and do not separate. This is quite appropriate for something cut or thrust with a sword: the sword is not bouncing off the target, instead it goes all the way through it or gets stuck in it. For true impact weapons, maces and sticks for example, this is more debatable but can still give an idea of the maximum deformation incurred; when it is reached weapon and target are moving together at the same speed, only then being separated again due to elastic forces.

Global balances

Before delving into the details of what happens during impact, there are conclusions that can be reached by simply considering global balances of momentum and energy before and after impact.

Conservation of momentum brings up the final speed of mass and target (assumed to be identical, remember):
\[
v_f = \frac{m_w}{m_w + m_i} v_0
\]

This final speed allows us to compute a kinetic energy balance. The kinetic energy of the system is not conserved. There will always be less kinetic energy in the system after the impact than before. This is a property of inelastic impacts; kinetic energy is dissipated in sound, heat, and damage for example. Knowing the final speed, we can compute that dissipated energy. It is:

\[
E_d = \rho E_0
\]

Where \(E_0 = \frac{1}{2} m_w v_0^2\) is the initial energy of the weapon, and
\[
\rho = \frac{m_i}{m_w + m_i}
\]
is a reduction coefficient which represents the effect of relative masses between weapon and target.

In the best cases, when the ratio \({m_w/m_i}\) is very small, the whole initial energy is dissipated. However in most practical cases, the reduction coefficient is less than 1. It reflects the fact that a light target will rather be moved than damaged. This reduction coefficient is a significant insight, because it puts a cap on how much energy can be used to damage the target. Damage will not always be directly proportional to dissipated energy, as we will further detail in the next part. Irrespective of this, the reduction coefficient will always show up. Another way to look at it is that the impact happens, relative to the target, as if it was hit by a weapon of mass \(\rho\,m_w\). So when you hit a mosquito (\(m_i \simeq 2.5\times10^{-6}{\rm kg}\)) in the air with your hand (\(m_w \simeq 0.6{\rm kg}\)), it actually sees it with a mass of only \(\rho\,m_w \simeq 4.2\times10^{-6}{\rm kg}\). Which explains that it is absurdly hard to kill a mosquito in the air with a hand strike, while it is trivially easy if the mosquito is resting on a wall. Being on the wall gives an enormous effective mass to the mosquito, which then sees the whole mass of your hand.

Looking at that reduction factor, one might conclude that the best weapon is an extremely light one. Indeed in this case the reduction coefficient is around one, no matter the target mass. This is pretty much the basic idea behind bullets: extremely energetic projectiles with light mass. However, hand propelled weapons hit a limit here. In order to put a given amount of energy into a very light weapon over the course of a strike, you’ll have to increase power significantly, because of how fast the weapon moves. Human muscles have a limited power and speed of contraction, and therefore retaining some mass is necessary. This effect will be the topic of a next article!

Modelling damage

Now let us consider how to model what happens during the impact in more details. We will consider that at time \(t = 0\), the weapon contacts the target, and pick points of reference \(x_i\) and \(x_w\) on the target and weapon, respectively, coincident at \(t = 0\) (i.e. \(x_i(0) = x_w(0)\). Starting at that moment, the weapon applies a force \(F\) to the target (and conversely, the target applies an opposite and equal reaction \(-F\)).

We will use \(x_r = x_w – x_i\) as a variable. This is the position of the weapon relative to the target. The equation governing the system is then:

\[
\rho\,m_w \frac{{\rm d}^2 x_r}{{\rm d}t^2} = -F
\]

We can define damage as the penetration depth into the target. The impact ends at the time \(t_f\) when \(\frac{{\rm d} x_r}{{\rm d}t} = 0\) (target and weapon are moving at the same speed), and the damage is taken as \(d = x_r(t_f)\). The next question is how we model the force response between the weapon and target. Depending on the behaviour, we will see in the next three parts that the expression of the damage can be widely different.

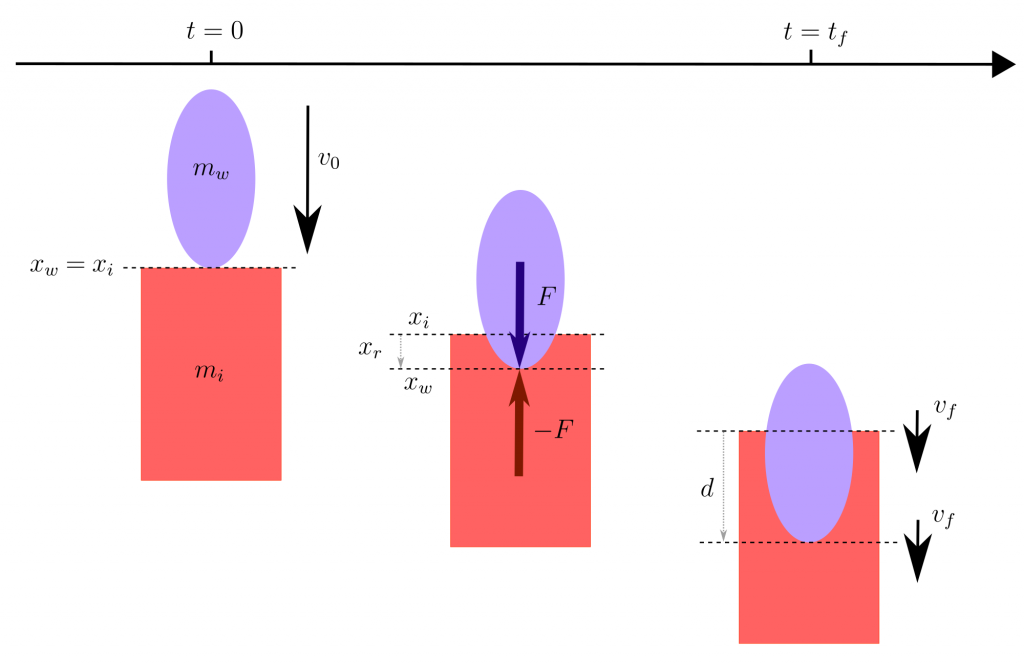
The model of what happens during the impact, between \(t = 0\) and \(t = t_f\). The variation in relative speed between weapon and target determine the penetration depth \(d\).

Constant resistance

In the simplest case, we can suppose that the target resists with constant force as the weapon moves into it. So we simply have a constant \(F = F_{max}\). In this case:
\[
d = \frac{\rho E_0}{F_{max}}
\]

Damage is proportional to the dissipated energy. This corresponds to the behaviour noted in 1721 by Willem ‘s Gravesande, in an experiment that was fundamental for our understanding of kinetic energy. However, not all materials will respond like this.

Depth-dependent reaction

There are cases where it is clear that the previous model is not realistic. In a thrust, for example, you have an increasing portion of the blade in contact with the target as it goes deeper. If you assume that most of the resistance comes from friction on the blade, the total force will be proportional to the depth of penetration at any given time:

\[
F = k_d x_r
\]

with \(k_d\) a coefficient modeling the toughness of the target. The greater \(k_d\) is, the tougher it is to pierce the target.

In this case, penetration depth is not proportional to the dissipated energy, but to its square root:

\[
d = \sqrt{\frac{2 \rho E_0}{k_d}}
\]

Some preliminary experiments, dropping a dagger into the ground, indicate that this can be a proper model. Doubling the dagger’s energy, either by dropping it from twice as high or doubling its mass by fixing a roll of steel wire unto it, does not double penetration, instead multiplying it by roughly \(\sqrt{2}\). I need to refine that experiment to make a more proper study: make sure the ground is homogeneous, make sure the dagger goes in straight without rotating in the air before landing.

Fluid friction

In both previous cases, the damage was determined purely by dissipated energy. This is not always the case; here is a model that shows a different behaviour. We will consider a target that resists to speed rather than depth, like so:

\[
F = k_f \frac{{\rm d}x_r}{{\rm d}t}
\]

This is, for example, how a viscous fluid responds at speeds that are below the threshold of turbulent behaviour. I do not think it is a common response at the speed reached by swords, in the medium of most targets, but it is nonetheless interesting as a theoretical example to show the diversity of behaviours. In this case, the damage can be expressed as:

\[
d = \frac{\rho\,m_w v_0}{k_f}
\]

Damage is proportional not to weapon energy, but to momentum. In this sort of impacts, mass takes up more importance. An important thing to remember is that the impact has no real end in this case: relative speed between weapon and target is exponentially decreasing, but never reaching zero. The collision is very ‘soft’, so to speak, which is a possible argument against the use of this model for most real-life impacts.

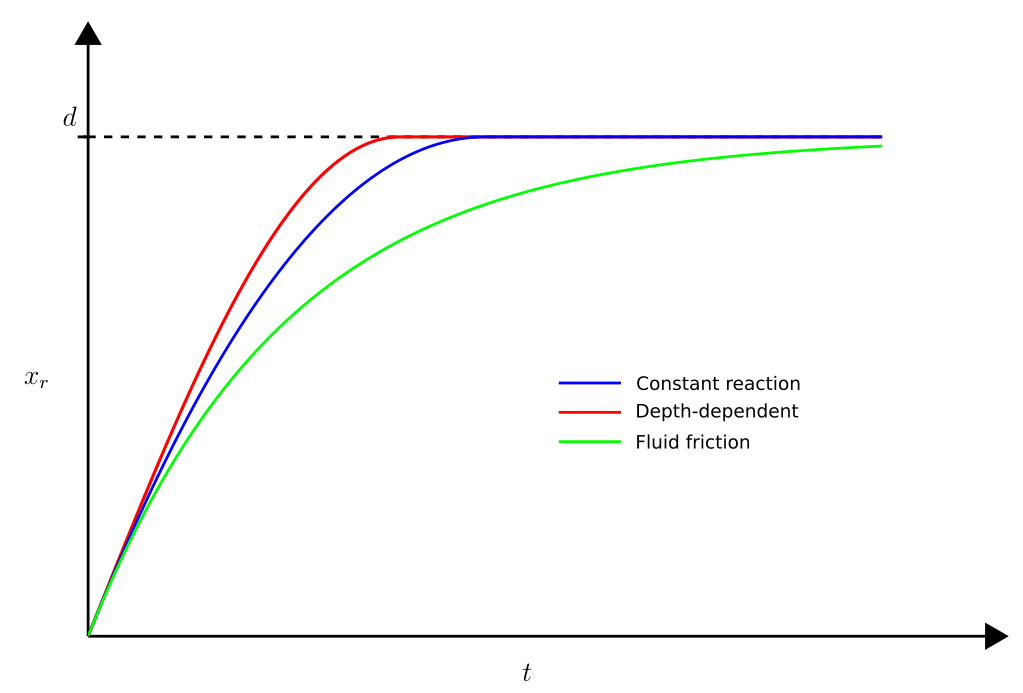
A comparison of the three impact models that have been described. Parameters were picked to have the same initial speed, and same final depth of damage. The sharpest impact is given by the depth-dependent model, and the softest is given by fluid friction.

None of these three models accurately represent the full complexity of the interaction between the weapon and an actual target. A target could exhibit a mix of all three behaviours, and more! The target could also be non-homogeneous, for example, which means that its behaviour would change discontinuously as it is penetrated. Target and weapon geometry can interact in a much more complex way. All of this make it extremely hard to come up with a precise predictive model of damage; there are simply so many unknowns and variables that every impact ends up being its own particular case.

Does this mean that this whole theoretical exploration is useless? Not so! It is always useful to be fully aware of the complexity of a phenomenon, if just to correctly identify the assumptions behind the various possible models. An awareness of the elements involved makes it easier to dispel oversimplistic or downright improper models of weapon damage. The problem simplification above remains pertinent although it can be further discussed. The global balances will always remain true, and the existence of the reduction coefficient will stand for all real-life impacts. In the two most plausible impact models (constant reaction and depth-dependent reaction) the dissipated kinetic energy determines the depth of damage. More experiments are warranted but in the meantime, using dissipated kinetic energy as a measure of damage seems a good idea.