This page is an introduction to the Weapon Dynamics Computer, a tool designed to document the dynamic properties of swords and other hand-held weapons. The tool was built by Vincent Le Chevalier, in collaboration with Peter Johnsson who provided design insights and precious sword data, during the preparation of the exhibition ‘The Sword – Form & Thought’.
The quality of a sword is often described by its metallurgical properties: the purity of the steel and the sharpness, hardness and resiliency of the blade. These are naturally important qualities for a weapon but the way it behaves when put in motion, how it responds to sudden changes in direction is equally or perhaps even more critical. A sword made of soft iron but with good balance will be a superior weapon to one that is made of fine steel of excellent temper but that is sluggish and unresponsive. It is often said that a good sword is like an extension of the arm, even though it would be more correct to say that it should be like an extension of the mind. This property of the weapon can be described as its balance. However, that word may bring to mind a balancing scale resting in static equilibrium which may not be the most apt image. Since swords are made for swift movements, we reach a better understanding by considering their dynamic properties. Some of the essential aspects that interact in establishing them are: mass, overall length, the proportion between blade and hilt, flexibility and perhaps most importantly how the mass is distributed along the length of the weapon.
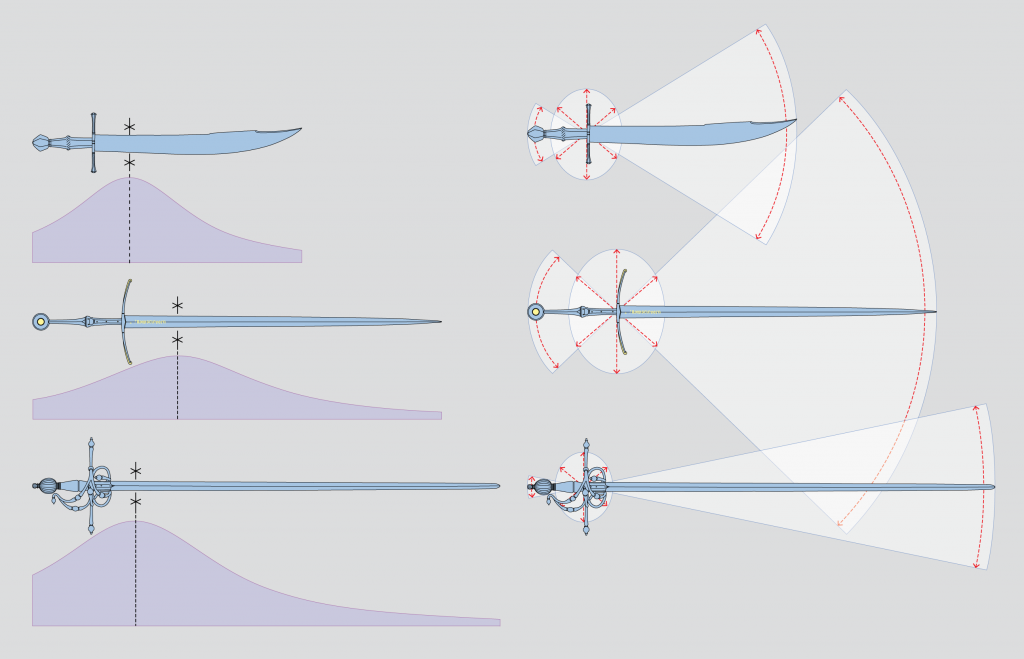
Effects of mass distribution
To get an intuition of the effects of distribution of mass we may imagine two bars of identical length, weight and point of balance. The first one swells at the ends while the second swells at the middle with pointed ends. If we were to put a spin to them we would find that the dumbbell shaped bar demands the most effort, while the one with pointed ends is more agile. Conversely, the dumbell shaped object will hit with more mass and deliver more powerful, albeit slower blows. Swords show the same kind of difference though generally not in the same magnitude.
These aspects are undoubtedly less accessible to the eye than the external shape and typology of the sword. Nonetheless they can be documented and communicated with the help of careful measurements and dedicated tools. By entering measurements into our Weapon Dynamics Computer, you will be able to produce graphs similar to those published in the catalogue of the exhibit ‘The Sword, Form and Thought’. We have attempted to make the tool and diagrams as objective as possible, not favouring one aspect of mass distribution over the others.
Effective mass curves and agility diagram of three very different swords
The graphs demonstrate agility by an oval and hourglass shapes. The shape and size of the oval describes the relative ease by which the hilt can be accelerated in a straight line in different directions. The hourglass shape describes the agility of the sword in rotation around the hilt. The size of the arc increases with increased agility. Of course, the motion of the sword in use will most often be a combination of these two basic modes of motion. The diagrams also include a curve of effective mass. The effective mass in any given location is the amount of mass that must be displaced to set that part in motion or to stop it in defence or attack. At the point of balance, it is the total mass of the sword and it will decrease towards the pommel and point, at a rate that depends on mass distribution. The goal is to obtain a numerical and visual representation of a sword balance, which can be related to our tactile impression sword in hand.
Necessary measurements
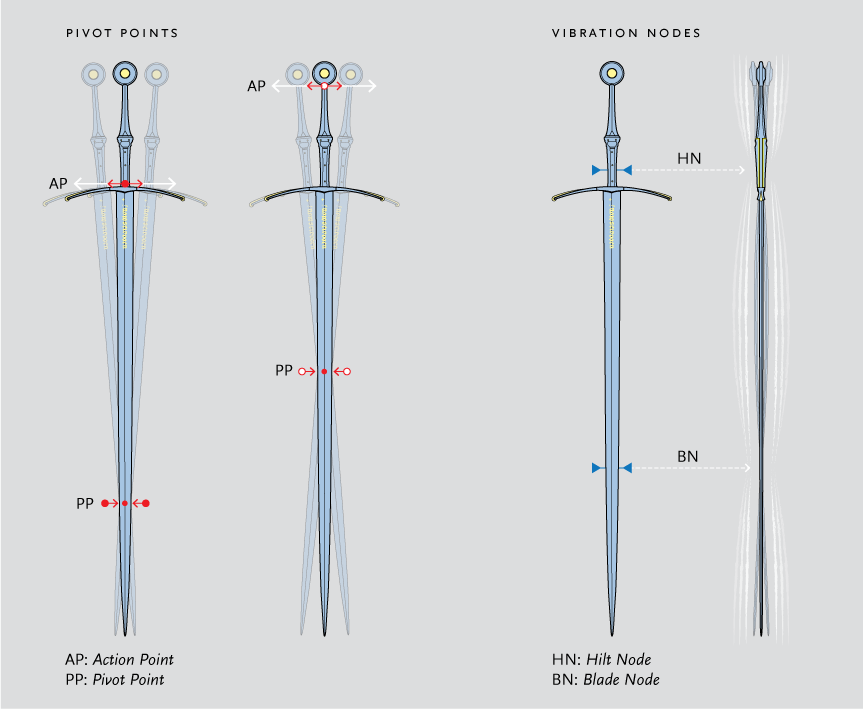
Measuring pivot points as accurately as possible is essential in order to acquire reliable information about mass distribution.
Pivot points occur in pairs and are an effect of the rotational inertia of the sword. Any given point along the length of the grip has a corresponding point in the blade. A method to observe these, called the waggle test, is to let a sword hang perpendicularly, pinched between two fingers. If the hilt is moved sideways back and forth a place in the blade will remain stationary. Depending on the action point (the point gripped), the pivot point in the blade will be found in different locations.
There are several mistakes that can disturb this measurement. First, if you pinch too hard and apply torque on your gripping point, it will unsettle the oscillation. That is why the grip must be as light as possible. Second, if the motion of your hand is not quick enough, there will be a motionless point on the weapon, but it will not be the actual pivot point that unlocks the properties of mass distribution. It is only when the frequency becomes high that the motionless point converges to the pivot point. Third, the motion of your hand should be as horizontal and straight as possible, otherwise the observation of the fixed point becomes very imprecise. The Dynamics Computer includes a correlation procedure that helps detecting measuring errors and mitigating their effect. We have found that a simple aid such as wrapping a hair tie or rubber band around the blade and adjusting its position until it seems to lie at the fixed point can increase precision.
If you are not confident in the waggle test, a simple device can be built to make pendulum tests. The tool can also use these as inputs.
When a sword strikes or is struck it will vibrate. There are two main places in a sword where vibrations are cancelled out. These are known as vibration nodes. The weapon appears to be stiffer when manipulated from these locations. In the majority of swords from the high Medieval period to the Renaissance that the authors have studied and documented, the location of the vibration nodes of the hilt and the blade are also nearly corresponding pivot points. This makes the blade node suited for especially powerful blows, creating a “sweet spot” there. Therefore the effective mass at the blade node gives a good idea of how much mass the sword would hit with.
Measuring two pairs of pivot points from different hilt location, and the nodes.
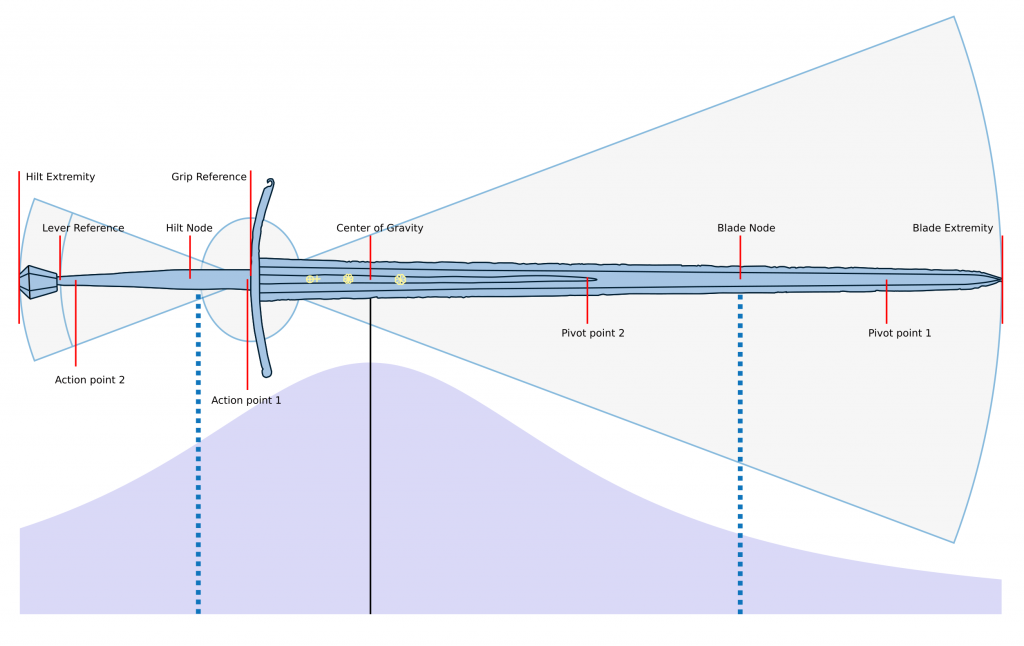
The other measurements needed to fill the Dynamics Computer are straightforward and well known. Here is an example of a complete set of measurements.
All the points measured on a sword to document its dynamics
They are further explained in the accompanying Walkthrough. We hope you will enjoy building graphs for the swords you come across, and sharing them with the world!
The text and images on this page are © 2017 Peter Johnsson and Vincent Le Chevalier, All Rights Reserved