Since the Weapon Dynamics Computer has been made public, there has been some criticism of the choice of the waggle test to measure moment of inertia (or equivalently, radius of gyration). The waggle test is tricky to get right, and the study of Robert Geißler has made it clear that it can be both biased and unreliable. I would argue that with training and carefulness, the waggle test can be reliable and precise enough to document hand-made objects. However, not everyone has the time or incentive to get to that level, and even then it is good to have another method of measurement to check the result and make sure that the collected data is trustable.

In industry, moments of inertia are often measured and the methods for that are well-known. All rely on the same principle, which is to build a pendulum including the object to measure, and observe its period of oscillation. Depending on the setup used, you then use different formulas to deduce the moment of inertia from the period of oscillation. These methods often involve precisely designed and manufactured apparatus, that make it possible to reach a very high precision and measure around several axis. As a downside, they can be cumbersome and costly (to the point that I have not found a public price for many of the devices, which is rarely a good sign cost-wise). Although they might be used on swords, they are not well-adapted to that specific problem.

Swords are hand-made, by processes that are inherently not of industrial precision. Sword documentation can therefore cope with some uncertainty, bigger than for industrial parts. Swords must often be documented “on the field”, with fairly little equipment, and in conditions that do not put undue stress on the object, nor fear in the owners (private or museums). The waggle test fits that bill, being done with hands and eyes, but it involves the human doing the test a bit too much. Pendulum tests have less avenues for human error. My guiding idea has been to design a way to make a pendulum test with as little equipment as possible, accessible to as many people as possible, but at least as accurate as the waggle test is for me.

Here is the list of constraints I wanted to satisfy with my own device:

• Low cost, low practical skill needed to build the setup and use it
• Low weight, portability
• No calibration needed, no corrective factor due to the specific setup
• Can adapt to any sword (or weapon) shape, without putting too much stress on the object
• Can measure oscillation period from several precise points (just as can be done for the waggle test)

Principle

Swords are specific in two ways. First, their center of gravity is close to the hilt. Second, they have a blade that is by definition quite thin compared to the handle. Considering these two aspects, I realized that having the sword oscillating hilt down was going to be easier: there is more impetus keeping it going that way, as the center of gravity is further from the center of rotation. Also, it is relatively easy to setup a well-defined, measurable and stable axis of rotation by laying the blade flat against some form of edge. Although the axis of rotation established in this way is at the surface of the blade, it is not far from the central axis of the weapon, close enough to make a very small difference.

The principle of my pendulum device is therefore described in this way:

• A support edge is protruding horizontally from a fixed surface, that of a table for example
• The sword is suspended hilt down, flat against the support edge, from thin wires passing over the support edge at a certain distance from the sword
• An additional contact wire is passed around the blade and pulled to the support edge to keep the blade in contact with it

The thin wires add negligible inertia to the object measured. The contact wire should apply just enough pressure to keep the blade in contact, which isn’t much at all in normal oscillations, and therefore does not overly disturbs the measurement either. The support edge materializes the axis of rotation in such a way that it is very easy to see and measure where it lies on the weapon. Therefore this setup achieves the goal of timing only the motion of the sword, without needing any calibration or correction. It is also of course adaptable to any sword shape, as there is no part actually gripping the sword and wires can be attached in any way necessary. Fairly little stress is applied to the weapon, as the support edge can be made of relatively soft material such as aluminium. By varying the length of the wires, you can make the sword oscillate around several points and correlate the measurements.

The next part details my practical implementation of the idea, which achieves the first two goals as well!

My pendulum setup

The core of my device is formed by a simple plank. On one side, I fixed a small portion of flat aluminium profile that serves as a support edge. It protrudes slightly from the board. Aluminium is soft enough not to scratch steel swords, and can be further cushioned by a thin cotton cloth for the most precious items. I have filed it slightly to get a finer edge (this should not be overdone as the support edge must remain stiff enough not to deform under load). The upper surface should remain flat. The device is layed on a table, lested or clamped to it.

Full view of the pendulum setup. The board is lested by a water bottle, which is enough to counterbalance most swords.

The support wires are simply fixed on nails driven into the plank. In order to adjust their length more easily, they are doubled as shown and a can be shortenned through a simple self-locking device made from two rings. They also go through a small net (taken from a bird feeding fat ball) that can support the bottom of mostly anything sword-shaped. Support wires should have two qualities: they should be inextensible, and they should be flexible as they will have to bend at a sharp angle around the support edge.

A close-up from above the support edge. In my device, there is in fact one support wire that starts on the board, goes down over the edge, around the hilt, up again, to the other side, down and up, and finally into the self-locking device.

A view of the hilt supported by the wires. The wires go around the hilt as needed, and the sword’s pommel is wrapped in the small net.

The contact wire is a simple loop that goes over the sword’s tip, and is pulled by a rubber band fixed to the middle of the plank. Several nails are driven into the plank at small intervals, providing a way to adjust the tension in the contact wire. It should be just tense enough to prevent the sword from leaving the support edge. The wire should be in contact with the support edge, never hovering above.

A close-up of the contact wire, pressing the sword on the support edge. The contact wire should touch the flat surface of the support edge, to be as close to the center of rotation as possible.

The whole thing comes at a very low cost, and is quite possible to carry around, even moreso if you are already carrying swords.

The sword is installed by placing the pommel into the net, then putting the flat in contact with the support edge and securing the contact wire. Once it is secure, you can see it oscillating!

Using the tool

The Weapon Dynamics Computer filled with pendulum tests data

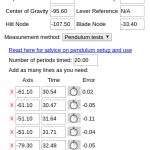
The Weapon Dynamics Computer now has an option to measure via pendulum tests. In addition to the usual measuring tools, you will need a stopwatch. Most phones or watches include one, but for convenience the tool includes a stopwatch on each pendulum test line as well. Just press the button and the stopwatch starts (the button becomes red). Press it again, and the stopwatch stops, and a dialog pops up for confirmation. If you accept the measurement it is automatically reported in the text field (be careful not to erase previous measurements!).

The first thing to decide is how many periods of oscillation you are going to time. Indeed, if you want a pendulum test to be more accurate than the waggle test, you will need to reach a fairly good precision on the measurement of the period, and timing many allows you to narrow down the value. I am personally using 20 as a default; assuming a timing accuracy of 0.1s, the measure of one period is then to 0.005s.

You need to measure precisely the position of the axis of rotation, and then enter a time. You can do this from several points, varying the length of the support wires, or even several times from the same point. The tool will take all the measurements into account and come up with the value of the radius of gyration that fits best all of your observations. It will also display the error value for each measurement, allowing you to see if you are being precise enough. The computed uncertainty on the radius of gyration should be quite small: I have reached less than 2mm on every example so far.

You can look at some examples of my results in this example database. Note that you can enter measurements via waggle tests and pendulum tests for the same sword, and switch and compare as you like. All the swords in this database were measured using both methods. As you can see, on some swords I have been wrong with the waggle test, but on many the results are comparable. I should eventually publish a more thorough analysis of the differences between these results.

In the same database you will find data about a plain uniform steel profile (1m long, 3cm wide, 2mm thick). The pendulum data is what I have measured with my setup. The waggle test data is theoretical: the pivot point I have entered is the position that can be computed based on the dimensions of the profile. As you can see there is a small bias: my estimate is a radius of gyration of 28.65cm ± 2mm, and the theoretical value is 28.87cm. At this level of precision it is hard to tell whether the difference comes from a bias in my setup, a bias in my observation of the period, or if the steel profile is not perfectly true to its theoretical equivalent (slight variation of thickness or density). In any case, it seems to me that this degree of precision is sufficient for sword analysis!

Error causes

What are the ways in which my setup can fail? There are of course many, but here are some I have noticed.

• The lighter the object, the more friction and traction from the contact wire will become important. This will eventually be enough to severely disturb the measurement. If you see that you cannot get 20 oscillations because of dampening, you probably have that sort of problems.
• Similarly, if the center of rotation is too close to the center of gravity, there will not be enough momentum to keep the object in motion. This can become a problem on very big swords, unless you get a higher support.
• The device does not really cope well with thick objects. In these cases the contact wire is going to disturb the oscillation a bit more, and the axis of rotation is further from the central axis of the weapon.
• Curved swords are of course more difficult to measure, as is already the case with the waggle test. Very curved swords will probably need an extended methodology to be measured accurately, taking the second dimension into account.

Conclusion

The device I have described is very accurate, for a very low cost. It is also more reliable than the waggle test, even for me, as someone who has been doing this for years. The downsides is that it cannot be improvised in the way the waggle test can, and that the raw results are harder to relate to: pivot points are something that you can experience in handling, a precise pendulum period from some arbitrary point on the blade is not.

If you are serious about measuring sword dynamics, it would at the very least be useful to build such a device to check that the waggle test gives you accurate results. By testing your device with a simple object such as a steel profile, you can make sure that it works as expected, and then by checking your waggle tests against pendulum tests, you will know exactly how well the waggle test works for you. If you are documenting rare swords as part of a planned research trip, having a working pendulum setup will spare you some trouble and uncertainty: once everything is set, even a single pendulum measurement will give more confidence in the result than two or three waggle tests, which can go wrong. The nagging thought that maybe the waggle test went wrong for whatever reason goes away.

I hope this article will be sufficient for all the interested people to build and use pendulum tests! Do not hesitate to ask questions in the comments…