Ceci est une version française de cet article, suite à des demandes de lecteurs intéressés !
La distribution de masse est une composante bien connue de la performance et de la perception que nous avons d’une épée. Bien que les fabriquants doivent utiliser toute une gamme de moyens pour la contrôler, seul trois paramètres sont nécessaires pour la décrire complètement du point de vue d’un utilisateur : la masse, le centre de gravité et le rayon de gyration. Ils sont bien connus des physiciens. Cependant, leurs valeurs ne sont pas directement représentatives de ce que l’on ressent l’épée en main. A cause de cela, leur utilité a été remise en cause et leur mesure est encore rare. Dans cet article, je vais montrer comment construire une représentation plus visuelle de la distribution de masse des épées, avec une application sur cinq épées de ma collection.
Dans cette version j’omets les démonstrations mathématiques, qui comportent peu de phrases de toutes façons, et je renvoie les lecteurs intéressés à la version originale… Une certaine familiarité avec cet article peut aider à bien comprendre certaines notions.
Les épées et leurs propriétés physiques
Pour exposer les représentations que je vais construire, j’ai choisi un échantillon d’épées que j’ai mesuré. Ce sont toutes des épées européennes à une main, mais chacune a un caractère différent qui s’explique en partie par la distribution de masse. La méthode est bien entendu générique et s’applique également à des épées tenues à deux mains, j’ai simplement choisi un échantillon d’épées que j’avais sous la main et qui présente une certaine diversité. Les voici (j’ai conservé les noms de la version anglaise pour rester cohérent avec les figures):
- A&A Milanese rapier
- L’offre standard d’Arms&Armor, achetée en 2004
- Darkwood rapier
- Une rapière que j’ai achetée en 2007, avec une lame d’entraînement. Plus de détails à son propos peuvent être consultés ici
- Albion Squire
- L’offre standard de la ligne Next Gen d’Albion Armourers
- AT Type XI
- Une épée faite par Angus Trim de type Oakeshott XI, en fait la première épée fonctionnelle que je me suis procuré en 2001
- Synthetic
- Une épée nylon à une main du Knight’s Shop (similaire à celle-ci mais de la première génération produite en 2010)
Comme je l’ai décrit dans un précédent article, les propriétés physiques pertinentes pour le comportement dynamique d’une épée, ses réactions aux forces et aux couples, sont au nombre de trois seulement : la masse totale, la localisation du centre de gravité (la position moyenne de la masse), et le rayon de gyration (qui représente l’écartement moyen de la masse par rapport au centre de gravité). Evidement, la fonction tactique de l’épée dépend aussi de sa longueur totale et de sa longueur de lame (que je mesure depuis la jonction entre les quillons et la poignée, appelée JQP dans la suite, jusqu’à la pointe). Ces paramètres fondamentaux sont donnés dans la table ci-dessous :
| Longueur totale (mm) | Longueur de lame (de JQP à la pointe, mm) | Masse totale (g) | Centre de gravité (depuis JQP, mm) | Rayon de gyration (mm) |
|
|---|---|---|---|---|---|
| A&A Milanese | 1090 | 956 | 1346 | 136 | 271 |
| Darkwood rapier | 1215 | 1072 | 1098 | 122 | 288 |
| Albion Squire | 980 | 820 | 1107 | 120 | 242 |
| AT Type XI | 980 | 845 | 1009 | 203 | 285 |
| Synthetic | 1065 | 885 | 764 | 168 | 262 |
Bien que toute l’information nécessaire soit là, il est très difficile d’interpréter les chiffres. Comparer les valeurs numériques des propriétés indépendament ne donne pas réellement d’information sur les sensations qu’un utilisateur peut avoir. Les longueurs sont assez simples à interpréter, mais les paramètres de la distribution de masse sont obscurs. Vous devez me faire confiance sur ce point, puisque cela ne peut être démontré que les épées en main. Par exemple, bien que la Milanese rapier soit la plus lourde de toutes, elle est en fait plus agile que la type XI. La Squire a un centre de gravité aussi proche de la garde que la Darkwood, mais est en fait plus lourde de lame. Les rayons de gyration sont encore plus délicats à interpréter, au point que je peine à proposer un exemple de ce que l’on pourrait en conclure…
Plus que les paramètres eux-mêmes, ce sont leurs interactions qui définissent le sentiment de l’arme, et ces interactions ne sont pas bien représentées sur une table comme celle-ci. Le problème est aussi multi-dimensionnel, et la construction d’une représentation intuitive et visuelle serait d’une grande aide pour l’analyse rapide, la comparaison et la communication des résultats. C’est ce qui m’a mené aux développements décrits dans les deux parties suivantes.
Equivalent à deux masses
Au moment où j’ai appris comment déterminer des centres d’oscillation, une idée toute naturelle a été de les utiliser. Si l’on choisit un point de pivot et qu’on trouve le centre d’oscillation associé, un système de deux masses peut être construit : une à chaque point, relié par une baguette sans masse. On peut calculer les valeurs des masses de sorte que ce système ait la même masse, le même centre de gravité et le même rayon de gyration que l’épée. Cela signifie qu’il réagirait aux forces exactement de la même façon que l’épée, il lui est en ce sens équivalent. Il va sans dire que ce système est beaucoup plus facile à appréhender que la distribution de masse complexe d’une épée, et est aussi plus intuitif. Ceci était la motivation de mon précédent article.
J’ai choisi de placer l’une de masses ponctuelles à la jonction quillons-poignée, car c’est un point de référence précis et significatif (notre main se positionne naturellement par rapport à ce point lorsque l’on saisit l’arme). Les seuls paramètres restants sont donc la masse aux quillons, la masse sur la lame, et la position de cette masse mesurée depuis la JQP, que j’ai appelé longueur dynamique. Voilà le résultat dans une table :
| Masse aux quillons (g) | Masse de lame (g) | Longueur dynamique (mm) |
|
|---|---|---|---|
| A&A Milanese | 1074 | 272 | 674 |
| Darkwood rapier | 931 | 167 | 801 |
| Albion Squire | 888 | 219 | 606 |
| AT Type XI | 670 | 339 | 604 |
| Synthetic | 542 | 222 | 577 |
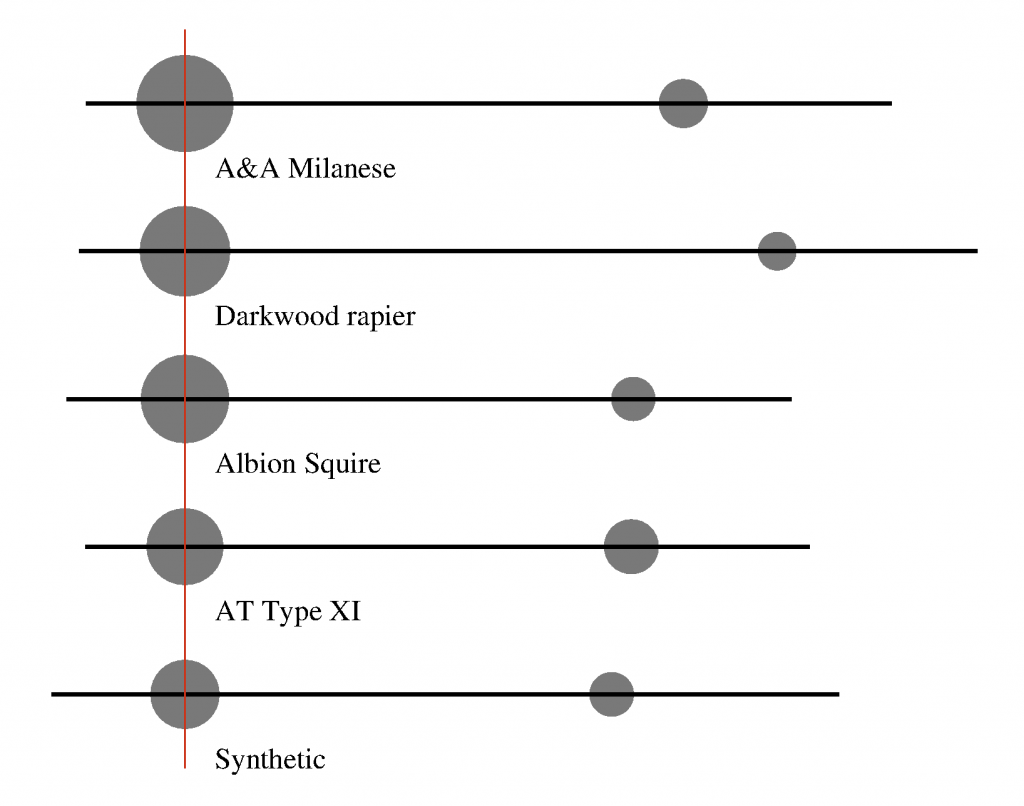
Une fois traitées ainsi, les données se prêtent aussi très bien à une représentation graphique ! La voici :
La ligne noire représente l’axe longitudinal de l’arme. La ligne rouge matérialise la jonction quillons-poignée, les épées sont alignées sur ce point. Les aires des cercles gris représentent les masses aux quillons et sur la lame, et les deux masses sont séparées de la longueur dynamique.
Ce système de deux masses est bien plus représentatif que les données brutes ; on voit comme la rapière a une faible masse de lame, alors que la type XI a la plus grande, avec les autres en intermédiaires. On a aussi une idée de la répartition de la masse entre la garde et la lame, la rapière étant plutôt à garde lourde et la type XI à lame lourde. La longueur dynamique est un peu plus délicate à interpréter, mais dans les grandes lignes plus elle est longue, moins l’épée a tendance à suivre les mouvements de coupe (pensez à ce qui se produit en manipulant un bâton long ou court, le court se réaligne bien plus vite). Un autre avantage est que cette représentation peut être mesurée directement sans aucun calcul. Même en partant des données dynamiques de la section précédente, le calcul est facile, et là encore décrit dans mes articles précédents.
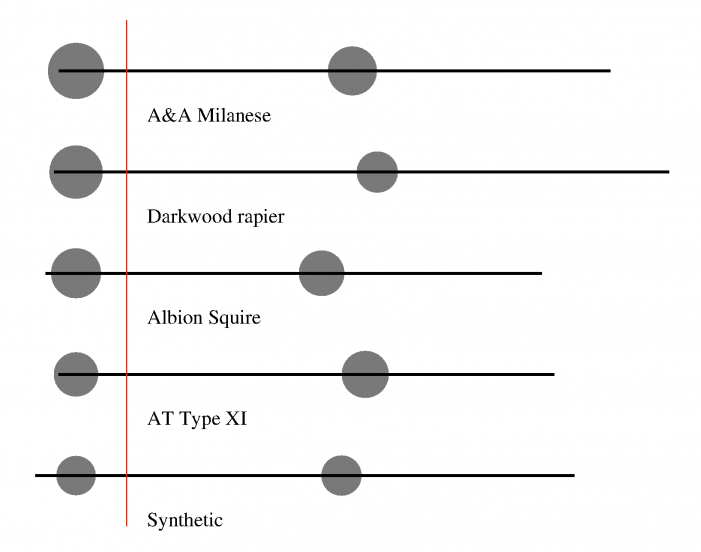
Cette représentation souffre cependant de trois inconvénients majeurs. D’abord, elle donne une fausse impression à cause des deux masses ponctuelles : en les voyant on s’imagine que la masse de l’arme est réellement concentrée en ces deux points, ce qui n’est pas vraiment le cas. Ensuite, elle ne tient pas compte de l’étendue physique de l’arme : la masse de lame pourrait tout à fait se trouver au-delà de la pointe (ceci se produit sur des fleurets, que je n’ai pas inclus dans mon échantillon). Enfin, elle nécessite un choix arbitraire. J’ai choisi la JQP comme point de pivot, mais le modèle peut être construit depuis n’importe quel autre endroit et être toujours représentatif. Par exemple, voilà le résultat si on prend un point sur la poignée à 10cm des quillons comme référence :
Lequel est le plus correct ? Rien ne nous permet de faire un choix. Le fait que la représentation dépende aussi radicalement de ce choix arbitraire n’est pas satisfaisant. Il nous faut une représentation unique pour chaque épée, et qui fonctionne tout de même pour n’importe quelle épée.
Bâton et masse ponctuelle
La représentation suivante est basé sur un objet intuitif courant qui a à la fois une masse et une longueur : le bâton. Le bâton uniforme pour être précis, doté d’une épaisseur constante sans amincissement d’aucune sorte. On ne peut pas trouver beaucoup plus simple qu’un bâton de ce genre, et c’est un objet familier que chacun est capable d’utiliser quasiment intuitivement dès le plus jeune âge. Un bâton uniforme est toujours bien équilibré quel que soit l’endroit où il est tenu, et est très facilement décrit par sa longueur et sa densité (à quel point il est ‘costaud’).
Les épées ne sont assurément pas des bâtons. Cependant, il est possible de trouver mathématiquement à quel point elles en diffèrent en divisant leur masse en deux parts :
- l’une dans un bâton uniforme de même longueur que l’épée
- l’autre concentrée (ponctuelle) quelque part sur l’axe longitudinal de l’arme
Le calcul est un peu plus délicat que pour le système équivalent précédent, mais reste possible de manière exacte et explicite. L’utilisation d’une masse ponctuelle assure que nous attribuons le maximum de masse au bâton. On a donc trois paramètres :
- la densité du bâton
- la concentration de masse (le rapport entre la masse ponctuelle et la masse totale)
- la localisation de la masse ponctuelle (qui peut être donnée relativement à n’importe quel point de référence sur l’arme)
Bien sûr on pourrait choisir d’autre combinaison de ces paramètres, mais mon expérience personnelle m’a conduit à les choisir car ils représentent au mieux ma perception tactile des épées. Voici la table :
| Densité du bâton (g/m) | Concentration de masse (%) | Localisation de la masse ponctuelle (mm, depuis la JQP) |
|
|---|---|---|---|
| A&A Milanese | 422 | 66 | -7 |
| Darkwood rapier | 260 | 71 | -16 |
| Albion Squire | 435 | 62 | -11 |
| AT Type XI | 612 | 41 | -19 |
| Synthetic | 317 | 56 | 22 |
Et une représentation graphique des données :
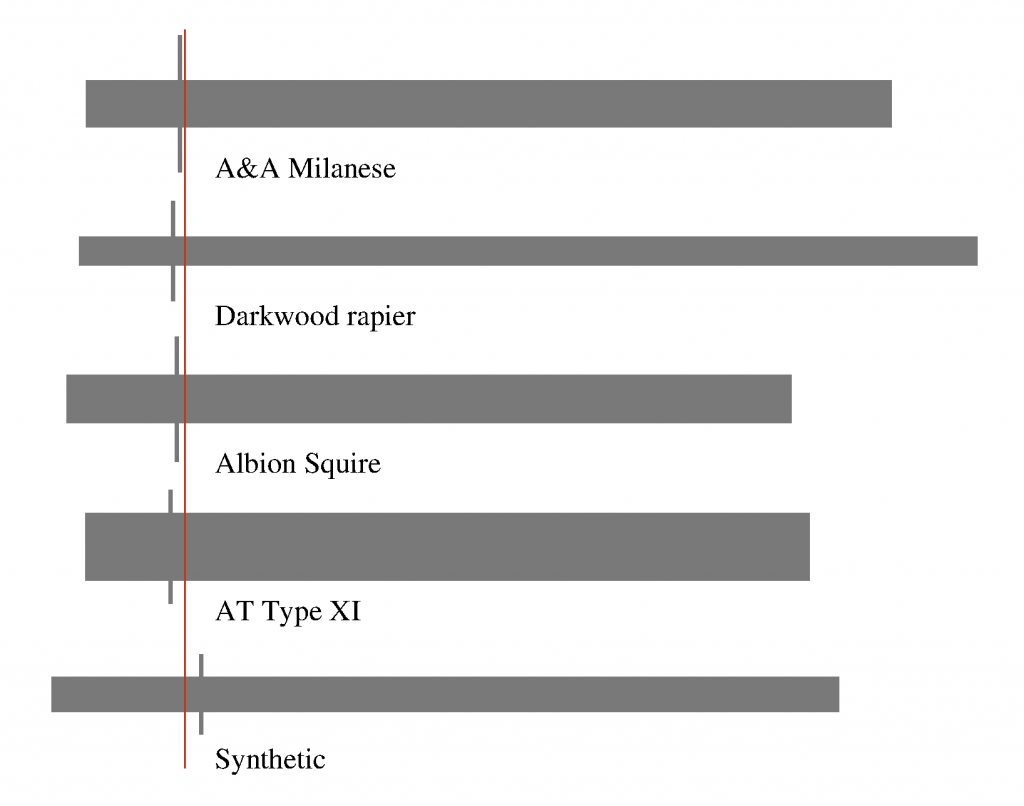
Une représentation graphique de l’équivalent en bâton et masse ponctuelle des épées de l’échantillon
Ici les rectangles représentent la masse du bâton : leur épaisseur est proportionnelle à la densité. Les barres verticales grises marquent la localisation de la masse ponctuelle. Le rapport entre la longueur de la barre grise et l’épaisseur du rectangle donne la concentration de masse pour chaque arme. Notez que la représentation est ici entièrement objective, la seule part de subjectivité vient du choix d’alignement des armes (ici j’ai conservé la JQP). La représentation est unique pour chaque arme.
Sur ce graphique, la rapière apparaît exactement comme on la ressent : un long et fin bâton avec une forte concentration de masse à la poignée. La type XI est presque l’opposé : un bâton massif et peu de concentration de masse dans la poignée. La rapière Milanaise et la Squire ont des densités très proches, et en effet leur ressenti est assez proche en terme de substantialité. Le simulateur en nylon a à la fois un bâton plus léger et une plus faible concentration de masse, ce qui explique que sa manipulation ne provoque pas les mêmes sensations.
La localisation de la masse ponctuelle est particulièrement intéressante à considérer. Observez comme elle est proche de la JQP sur les 5 armes. Ceci est remarquable, car les fabriquants n’ont en aucune façon utilisé cette représentation et ont donc abouti à ces résultats en ne considérant que le ressenti et l’historicité. J’ai calculé cette localisation pour de nombreuses armes mesurées par d’autres personnes et par moi-même, et cette observation reste globalement pertinente : les épées sont équilibrées comme des bâtons avec une grande masse ponctuelle attachée près des quillons. Bien sûr la localisation précise varie et est importante, comme je le décrirai dans de futures articles. Brièvement, on peut dire que les armes qui ont la masse ponctuelle plutôt vers la lame ont tendance à tourner vite en mouvement de coupe et sont plus difficiles à contrôler, alors que celle qui l’ont dans la poignée sont plus stables mais du coup partent moins vite dans la coupe. Une masse ponctuelle trop près du pommeau ou trop avancée sur la lame semble donner un mauvais ressenti à l’arme pour des raisons opposées, respectivement trop stable ou pas assez. Incidement, cette relative invariance de la localisation de la masse ponctuelle plaide pour l’utilisation du premier des deux systèmes de deux masses de la partie précédente, la JQP paraissant avoir un rôle “central” pour la distribution de masse.
Basiquement, la partie de la masse dans le bâton est ce qui cause une résistance aux mouvements de rotation, mais aussi ce qui frapper la cible lorsque l’on utilise le faible de l’épée. La masse concentrée à la garde augmente l’impact des estocs lancés, et donne aussi une plus grande stabilité aux parades prises au niveau du fort. La majorité des gens ont la croyance erronée que la masse est concentrée dans le pommeau, parce que c’est une grosse masse évidente. Cette analyse montre que ce n’est pas le cas, et que la combinaison du pommeau et des amincissements de la lame a pour effet de concentrer la masse au niveau des quillons. C’est là une belle preuve de la difficulté du travail des fabriquants, qui doivent opérer conjointement sur la lame et la garde pour obtenir une distribution de masse correcte.
Cette représentation est sans aucun doute la plus utile que j’ai pu concevoir jusqu’ici. Le coût en calcul est plus que compensé par les informations nouvelles contenues dans les résultats. C’est une façon particulièrement efficace de communiquer l’équilibre d’une épée d’une façon intuitive, visuelle, concise et objective. Les seuls écueils à son utilisation à grande échelle sont les mesures et les calculs, et je compte bien contribuer à résoudre ces problèmes très bientôt !