The centre of percussion of a sword or impact weapon has at least three different definition, depending on the context and period. It can mean:
- the point on the solid where the impact is the greatest (this is somewhat imprecise, as we’ll see later)
- the point where an impact will impart no force to the hand
- the node of the primary mode of vibration on the blade
This has led to some confusion nowadays as to whether it is a useful notion and for what purpose.
In this post, I want to explore the history of the term: where it comes from, why was it called that way, what sort of people were studying it. The part 3 of the article Sword impacts and motions by George Turner is what gave me the impulse to study this topic. George Turner had some very good research, but maybe for lack of access to the original documents draw some exaggerated conclusions: for example that the scientists studying the notion were sword people, that the physical demonstrations were widely known and consciously used, or that the notion was meant to have a practical application to swords. I shall try to give a bit more context in what follows. I will start with scientific literature, where the term first popped up, and then explore the diffusion of that idea in the military and fencing literature.
I have inserted some mathematical asides in the course of the article, that are hidden by default. Please click if you want a more complete view! These make a heavy use of the vector calculations, some integrals, and are of course based on physical laws and ideas (linear and angular momentum, Newton’s laws of motion).
And they contain stuff like this:
\(
\mathbf{u} \times (\mathbf{v} \times \mathbf{w}) = (\mathbf{u} \cdot \mathbf{w}) \mathbf{v} – (\mathbf{u} \cdot \mathbf{v}) \mathbf{w}
\)
This is the formula for the double cross product, you will need it for the other asides!
In scientific literature
The study of the effects of percussions or impacts is a fairly hard scientific topic. Gaining a full understanding of these phenomenons necessitates the understanding of the laws of motion, but also of the deformations and elasticity of materials. It involves study of very big forces over a very short time, which is not easy to do when you do not have the appropriate mathematical tools. This took a long time, and I will try to show here how the notion of centre of percussion came to be. I have traced most of the information about the early stages from this edition in French of the complete works of Christian Huygens.
Aristotelian works
The journey begins in Ancient Greece. Sometimes in the fifth century B.C., a follower of the school of Aristotle wrote a small compendium of mechanical observations. The exact author is still disputed (read more details in this paper), but it is the rough date and text that we are concerned with here. As translated by Thomas N. Winter:
Problem 19
Why, if you put a large ax on wood, and a large burden on that, doesn’t it pull apart the wood, no matter how considerable the burden is? But if you raise the ax and hit with it, you split the wood even if you have less weight than you put on the ax in the first place? Is it because everything works through moving-power [greek: kinesis]? And the weight receives the moving-power of the weight more upon being moved than while at rest? So lying [on the wood] it doesn’t get moved the moving power of the weight, but receives it, and that of the striker, upon being carried.
Also the ax is essentially a wedge, and a wedge, though small, pulls apart large objects because of being two levers set in opposition.
The ancients were struggling to understand how objects in motion could be so much more effective than static forces. Remember that they had no clear distinction of speed, mass, weight, gravity, force and acceleration at that time, and very few mathematical tools to model what happens during the very brief time of the impact. Unifying the understanding of statics and of percussions would become an endeavor in itself. The famous Galileo experimented with impacts but failed to establish consistent laws. Contrary to what George Turner asserted, Galileo did not know how to model impacts, and did not study the center of percussion as far as I have found out. Additionally, his studies were destined rather to application in artillery than in swordsmanship… But let us leave the modeling of impacts for now and focus on that notion of center of percussion.
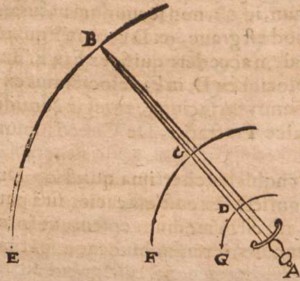
Baldi’s illustration of the sword problem. Point C here is the centre of gravity, which is not really realistic for a sword… Note that it is assumed that the sword rotates around the pommel in A.
The Aristotelian problem does not involve an optimal area to hit with (it is quite obvious for an axe). What would eventually become the centre of percussion apparently originates in a Renaissance commentary of the problem published by the Italian Bernardini Baldi in 1621 (starting at this page). Baldi expands on the axe problem, and considers a sword! He states that the sword blow is not most efficient in the hilt nor at the tip, but somewhere towards the middle, at a point he mistakenly considers as the centre of gravity. If the ashes of my education in Latin do not completely fail me, he seems to have understood an important trade-off: at the tip you have great speed but small mass, at the hilt you have great mass but little speed, and you need mass and speed to make an impact. The conclusion is wrong though, and one can wonder whether Baldi was really that familiar with swords, given how he misplaces the centre of gravity in the middle of the sword and seemingly has no personal experience of where the most damaging hits are done. As an aside, if you are looking for a source about swords filled with mercury to enhance their efficiency, this is one!
Mersenne’s question and Huygens solution
Marin Mersenne had a very active role in the scientific explorations of the 1600s, corresponding with scientists all over Europe, encouraging exchanges of ideas and submitting questions. Mersenne had read Baldi’s work; we know this for sure because he commented on his treatment of the question in his 1644 work Tractatus Mechanicus Theoricus et Practicus (p. 83). He disagrees that the maximum percussion happens either at the tip or at the centre of gravity, and further states that there cannot be a unique solution (presumably simply based on the length and centre of gravity), but that it has to depend from the exact shape of the sword, or object in general.
Ealier on, Mersenne also wrote letters about this topic to his learned friends; we have letters (or rather, very short passages thereof) from 1640 and 1643 by René Descartes about the sword problem. Descartes’ answers is interesting in that it points out that the answer might also depend on the wielder of the sword:
As for the greatest strength of a sword, I don’t doubt that it would be at the centre of gravity, if while giving the blow we would let go of it; and conversely, that it would be at the very tip of the sword, if it was held perfectly firmly, because the tip is moved faster than the rest. However, since it is never held so firmly, nor let go of entirely, that greatest strength is between the centre of gravity and the tip, and is closer to one or the other, depending on whether the user has a firm hand or not.
This is an interesting observation, but its validity is somewhat doubtful, and at that stage Descartes does not seem to have anything on the actual determination of a point of maximum percussion. He seems to be going by instinct as much as reason on this point; of all the scientists involved, he was perhaps the most familiar with swords and fencing, and trying to fit theory and experience on this front is not an easy matter.
Mersenne went on to experiment and reflect on the issue. With Descartes and Roberval he narrowed down the problem to the search of a point where all the momentum of the object was concentrated, that would be to a body in motion what the centre of gravity is for a static body, but both failed to express a general solution. They took into account that that then point of maximum impact depended on the centre of rotation of the object, and therefore considered objects rotating around a fixed point (although this is not strictly necessary, as the instantaneous centre of rotation would be sufficient). In 1646 a Jesuit named Honoré Fabri published his own treatise Tractatus Physicus de Motu Locali where he describes and computes the centre of percussion for specific simple shapes. This work is also the first, as far as I know, to use the actual term ‘centre of percussion’. In its ideas, it seems to be very close to Mersenne’s Reflectiones physicomathematicae (published in 1647). Both identify the centre of percussion with the centre of oscillation of the solid, though without much solid argumentation. They appear to be co-inventors of the phrase, though I did not find a sure indication that they had been in contact over that matter.
The centre of oscillation is nicely described in this letter from Mersenne:
I will only tell you that in practice, as soon as I want to find the centre of agitation [this is yet another name for the centre of percussion or oscillation] of a given body […] I take a pendulum that I can make longer or shorter in a moment with a slip knot, and as soon as I have found the length of string such that its vibrations are made in the same time as the suspended body, I conclude that this body has its center of percussion where the pendulum falls on it.
In other words, the object oscillates around the fixed point exactly as if all its mass was concentrated at the center of oscillation. The determination of that point actually had much greater implications than any study on swords might have had: it allows you to anticipate the timing of oscillations of any object, and this is used in clock making, paving the way to a more accurate determination of time. Note that in this period the term ‘vibration’ seems to be interchangeable with oscillation, nothing to do whatsoever with the flexibility of the object.
Christiaan Huygens, to whom that letter was addressed, is the man that would first propose a thorough and correct theoretical determination of the centre of oscillation on generic shapes. This was published in his treatise Horologium oscillatorium (1673). He also proved the identity of the two centres that Mersenne and Fabri had reported before.
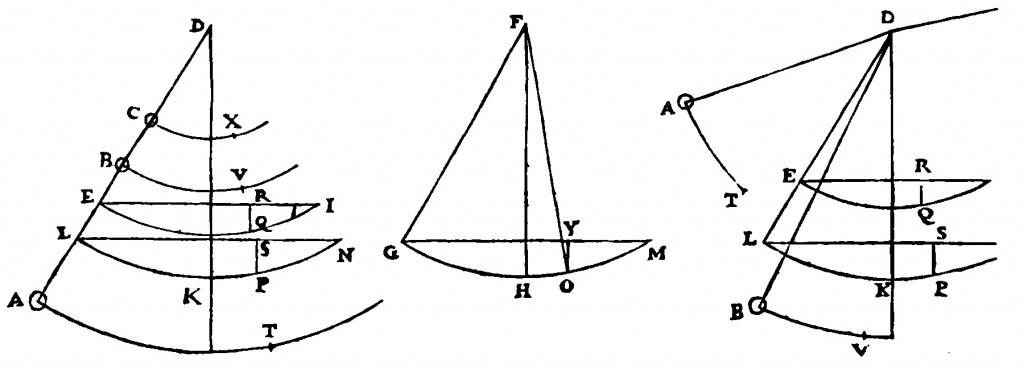
Huygens illustration of his method to compute the centre of oscillation. As you can see we are now quite far away from swords!
Essentially, they were proceeding by analogy with the centre of gravity, of which they had a much better understanding.
If you consider a solid \(S\), two-dimensional in the plane \(\mathbf{x y}\) for the sake of simplicity, gravity applies on each of its particle according to its mass. This produces leverage. The centre of gravity is a point where the sum of the leverages of all the forces applied to the particles is \(0\). Noting the position of the particle as \(\mathbf{X}\) and its mass \(\rm d m\), it is subjected to force \(\mathbf{F}\; \rm d m\), and we seek point \(\mathbf{G}\) such that:
\(
\displaystyle
\int_S \mathbf{XG} \times \mathbf{F}\; \rm d m = 0
\)
which boils down to
\(
\displaystyle
\mathbf{F} \times \int_S \mathbf{XG}\; \rm d m = 0
\)
This would actually define a line of acceptable points, but if we want it to work irrespective of the direction of \(\mathbf {F}\) (or equivalently orientation of the object), we need to have
\(
\displaystyle
\int_S \mathbf{XG}\; \rm d m = 0
\)
and then, noting \(M = \int_S \rm d m\) the total mass of the object, for any point \(\mathbf{O}\) we have:
\(
\displaystyle
\int_S \mathbf{OX}\; \rm d m = M \mathbf{OG}
\)
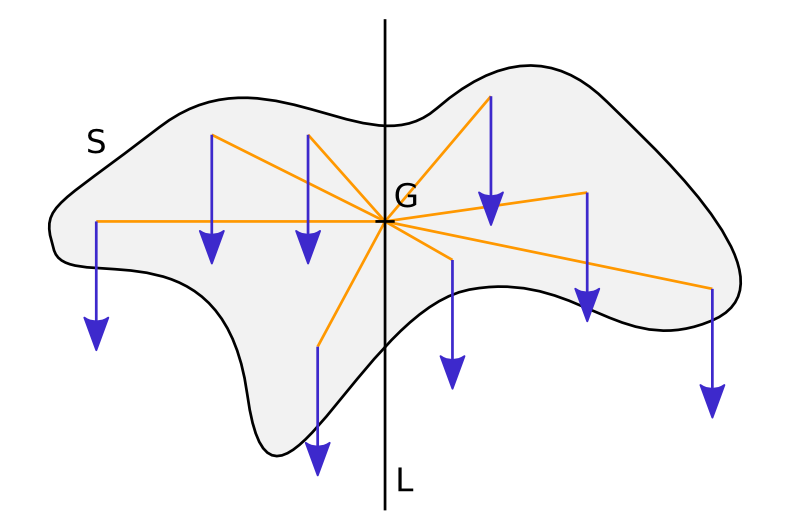
How to determine the centre of gravity of an object. The force applied to each particle of the solid S is represented by the blue arrows. The moment of all these forces around any point of line L is zero. Around point G, the centre of gravity, that property is true for any orientation of the uniform gravitational forces.
For the centre of percussion, they were using exactly the same principle. The only difference is that instead of considering the tiny forces applied by gravity at each point of the object, they were considering the momentum \(\mathbf{V} \rm d m\) of the particles, with \(\mathbf{V}\) the speed at each point. This makes sense, as momentum is the cause of the forces applied during an impact.
If we keep in mind that \(S\) is a non-deformable solid, at any given time it is rotating around some point \(\mathbf{R}\) with angular speed \(\Omega\). Thus the speed at point \(\mathbf{X}\) is given by \(\mathbf{V} = \Omega \mathbf{z} \times \mathbf{XR}\). We are therefore looking for point \(\mathbf{P}\) such that:
\(
\displaystyle
\int_S \mathbf{XP} \times (\Omega \mathbf{z} \times \mathbf{XR})\; \rm d m = 0
\)
which, thanks to the formula of the double cross product and the assumption of a 2D problem, simplifies to
\(
\displaystyle
\int_S \mathbf{XP} \cdot \mathbf{XR}\; \rm d m = 0
\)
Then, introducing \(\mathbf{G}\):
\(
\displaystyle
\int_S (\mathbf{XG + GP}) \cdot (\mathbf{XG + GR})\; \rm d m = 0
\)
and expanding:
\(
\displaystyle
\int_S \left( \mathbf{XG}^2 + \mathbf{GP} \cdot \mathbf{GR} + \mathbf{XG} \cdot (\mathbf{GP + GR})\right)\; \rm d m = 0
\)
then splitting the sum:
\(
\displaystyle
\int_S \mathbf{XG}^2 \; \rm d m + M \mathbf{GP} \cdot \mathbf{GR} + \int_S \mathbf{XG}\; \rm d m \cdot (\mathbf{GP + GR}) = 0
\)
Remember, by definition of the centre of gravity we have \(\int_S \mathbf{XG}\; \rm d m = 0\). So we end up with:
\(
\displaystyle
\mathbf{RG}\cdot\mathbf{PG} = -\frac{\int_S \mathbf{XG}^2 \; \rm d m}{M}
\)
Again this gives a line of acceptable points, but if we pick \(\mathbf{P}\) aligned with \(\mathbf{R}\) and \(\mathbf{G}\), it gives a unique point which is the centre of percussion of the solid in motion around \(\mathbf{R}\). What the 17th century early researchers were struggling with is the sum \(\int_S \mathbf{XG}^2 \; \rm d m\) here, as the mathematical tools to deal with calculation of the sort were in their infancy. This sum is the moment of inertia of the solid around \(\mathbf{G}\), an important data in the equations of motion.
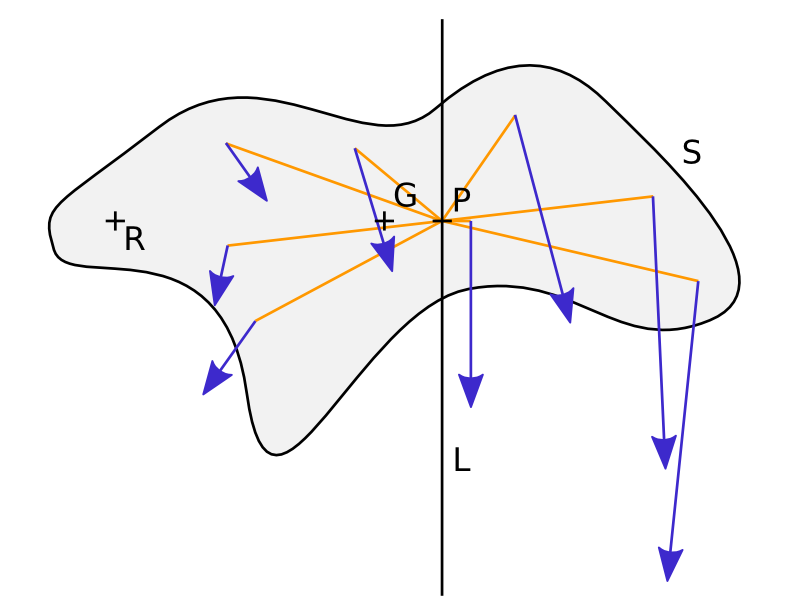
Defining the centre of percussion of a solid S in rotation around R. The blue arrows represent the momentum of particles of S. Around any point on line L, the angular momentum is zero. The centre of percussion P is the point on that line whose speed is aligned with that of the centre of gravity.
Of course none of this is truly a demonstration that the biggest impact happens at this point, or that the centre of oscillation has to be defined by the same formula. Huygens settled the demonstration of that last part, but the notion of biggest impact remained undecided as far as I have found out. I have found texts from the 19th century pointing out that depending on how you define biggest impact the centre of percussion may or may not be the location. The idea that the biggest impact had to happen here is due to the fact that the whole momentum (linear and angular) of the object can be reduced to \(\mathbf{P}\), as if there was just one big point mass in \(\mathbf{P}\). But momentum is only part of the story…
Diffusion of the notion
The notion of the centre of percussion eventually appeared in the Encyclopédie of Diderot and d’Alembert in 1751, still associated to the centre of oscillation, at which stage we can say that it had become widespread scientific knowledge.
George Turner is right that this was a famous problem; it was also initially about a sword, but swords were never meant as the object of any serious application by the scientists. It is also wrong to claim that the solution was well-known and predated that research. The determination of the centre of percussion and oscillation was a problem of theoretical physics, whose solution was only known of the few scientists involved in the discussion, at least until the 18th century.
Another point that must be made is that the centre of percussion equated here with the centre of oscillation does not always correspond to the greatest impact. This is because ‘greatest impact’ is actually a poorly formulated question. Depending on the mass and material of the target, as well as on the objective (moving the target, applying the greatest force, destroying it, etc.), the most efficient point can and will vary, and that is without even taking the user of the instrument into account. This was of little concern to our theoretical physicists, of course, who were using the question primarily to investigate the laws of motion. This should have been a primary concern of the fencers, however. We will now look at how the idea of the ‘centre of percussion’ transferred to military men and fencers.
In fencing literature
The parts of the sword according to Alfieri (1640). Cuts should be delivered by the part between D and E, consistent with Fabris.
[…]when executing a cut it is better to perform it half with the third and half with the fourth part [of the blade]; this way, the cut is twice as damaging as if it were delivered with the third part alone.
Salvator Fabris, Lo Schermo, overo Scienza d’Arme, trans. Tom Leoni
This implies that the hit has to be made somewhere around three quarters of the blade towards the tip. However, these texts do not use the term ‘centre of percussion’, nor do they dwell on the exact effect it has. It is still the case in Colonel Marey’s Memoir on swords etc. (1841, trans. 1860). That text has a curious observation, however:
In the cut, a sword should be considered in the light of a projectile, of which the portion in the neighbourhood of the point has a much greater velocity than the hilt. The hand gives it this impulse, and does not act by pressing the sword on the body to be penetrated at the moment of impact.
This describes a cutting technique where there is no transfer of force from the hand to the edge during the impact, with the momentum imparted to the sword doing the whole work. Interestingly, this is what happens when you hit with the centre of percussion associated to the hand, not to the centre of rotation. This is a departure from the original physical study, but the maths behind the centre of percussion also models it quite nicely. Colonel Marey does not do the link, though. It will only appear a bit later. Note that unless the centre of rotation of the sword is in the hand, the centre of percussion and the point of no hand shock will differ; the point of no hand shock is always at the same location, but the centre of percussion depends on the motion of the sword.
The term first pops up in military dictionaries. For example it is defined in 1758 in the French Dictionnaire militaire portatif, and the definition is found again in the English Military Dictionnary in 1805. In both cases, it is not specific to swords, and perfectly in line with the scientific meaning:
CENTRE of percussion, is that point in which the force of the stroke is the greatest possible. When the moving body revolves round a fixed point, the centre of percussion is the same as the centre of oscillation, and found by the same method; but when the body moves in a parallel direction, the centre of percussion is the same with the centre of gravity.
Arguably that notion was equally useful, if not more, to military engineers who had to build machines involving impacts. It is entirely possible that it was imported by these people, and only then applied to swords.
The first ever mention I have found of the consideration of centre of percussion being important to sword design is in a Note sur le nouveau système d’escrime pour la cavalerie (note about the new fencing system for the cavalry), by N.J. Didiez, published in Le Spectateur Militaire in 1834.
The whole effect produced by the blade has been attributed to mass alone, whereas this effect is found by mass and the square of speed. By putting most of the weight of the blade towards the tip, augmenting the distance between the centre of motion [centre of rotation] and the centre of gravity, the moment of inertia is augmented too, which considerably diminishes speed; moreover, the centre of percussion is moved, which makes the blow fall wrong, produces a reaction on the wrist, and therefore a loss of strength.
[…]
In the distribution of the mass, it is most important to consider the position that the centre of percussion should have.
In this text, we are exposed again to the tight link between centre of percussion and mass distribution, and also to the notion that impact forces on the wrist are bad, mirroring Colonel Marey’s observation.
N.J. Didiez was a professor of mathematics. You could argue that his use of the notion applied to swords does not prove that the military was using it in the same way. It did not take long, though: in 1842 there is extensive discussion of it in the Instructions théorique et pratique d’artillerie (theoretical and practical instructions of artillery) by Charles Victor Thiroux:
In the impact of any weapon, there is a point to consider, it is the centre of percussion: the action produced maxes out when this point hits the object that must be damaged.
The centre of percussion is, relative to the body in motion, what the centre of gravity is relative to the body at rest. It is easy to conceive that in a circular motion the parts furthest away have more speed, so that the centre of percussion must be farther from the fixed point than the centre of gravity.
Thiroux served in Napoleon’s army and was certainly a man of arms, although as a gunner the sword was maybe not his most familiar weapon. At this stage, I think it’s fair to consider that many military men would have heard of the centre of percussion at least, even if not everyone would understand its physical explanation or implications. That is almost two hundred years after the first appearance of the term in the scientific litterature…
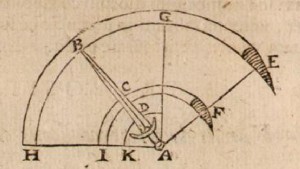
Just a bit later in 1844, Henry Wilkinson (a sword manufacturer) considers the centre of percussion in his production. There are a lot of swords from this manufacture which bear a mark on the location of the centre of percussion. How was this determined? The best explanation is found in a lecture by John Latham published in 1863 in the Journal of the Royal United Service Institution The Shape of Sword Blades. Here are the relevant parts:
Suppose you make a cut at a branch of a tree with the point of the sword, the probability is that your cut will produce very little effect, and you will feel a considerable jar upon the wrist and elbow. The same result will follow if you cut close to the hilt of the sword. In either case you waste a great deal of force, as is evident from the vibration you perceive in the blade, which represents so much force lost in the cut. If you go on cutting inch by inch along the whole length of the blade, you will at last come to a point where there is no vibration (Plate I. fig. 1, C. P.). This point is called the “centre of percussion,” and that is the point where the whole force of your blow will be effective, and where the greatest result will be produced on the body struck.
[…]
As I have explained, the centre of percussion can be experimentally ascertained by cutting inch by inch along the blade, and comparing the effect; but it is obviously of importance to have some means of ascertaining this point mathematically without the tedious process of experiment with every sword. This can be done by a formula, first proposed by Mr. Henry Wilkinson, and which is based upon the consideration of the properties of the pendulum. I have here a pendulum vibrating seconds in the latitude of London. Its exact length is 39.2 inches, and it consists of a very light wooden rod, terminated by a heavy leaden ball. In one respect it resembles the axe, as nearly the whole weight is concentrated in this one point. When I cause it to swing upon a fixed centre, I find it makes sixty vibrations in one minute; and I know that the centres of oscillation, of percussion, and of gravity are all concentrated within this leaden ball. If this were what is termed a mathematical pendulum, in which the connecting rod is supposed to have no weight at all, these three points would lie precisely in the centre of the ball, and from this point to the point of suspension is exactly 39.2 inches. Now, I hang up this regulation Infantry sword, fastening it as nearly as possible at the same point on which it would turn in making a cut, and I set it swinging upon this point, converting, in fact, the sword into a pendulum. You observe that the vibrations are very much quicker; if you count them, you will find that while the pendulum is making sixty vibrations the sword will have made eighty. Having obtained this point of comparison, our object is next to determine the length of a pendulum which will make the same number of vibrations which the sword has made, viz. eighty in a minute. By a very simple formula, I can calculate that the length of such a pendulum would be 22 inches. I measure this distance, therefore, from the point at which the sword was suspended and mark it on the back of the blade, and I shall find on cutting with it that this mark is the centre of percussion, where there is no vibration, and where I can cut the hardest with this sword.

Latham’s figure illustrating the centre of percussion (C.P.) and the centre of gravity (C.G.). This illustration will be used almost as-is by Burton later.
Although that text was published in 1863, I think we can assume that the ideas were already there in 1844 or just a bit later. This is an important text for several reasons. First, it describes a method for determining the centre of percussion of an object (here, a sword) that is pretty much verbatim what had been proposed by Mersenne in 1646 (see the quote in the previous section). Second, it introduces what would become the meaning of the term in the modern sword community: the point where there is no vibration, the node of vibration on the blade. This is a departure from the physical definition that only happened for swords, seems to have spread around this date, and seen a rebirth at the end of 20th century. It also points out again that there should be no repercussion to the hand.
As pointed out before, the point where an impact does not produce force on the hand only coincides with the centre of percussion if the sword is rotating around the hand. This physical bit allows us to clarify the ‘point on which it would turn in making a cut‘. If the sword was free of its motions, that no-shock-point would not necessarily be the point at which the impact is the greatest. I think some adaptation of the physical model were going on to better fit the experience: it seems that shock in the hand is detrimental to the control of the weapon, hence to the efficiency of cuts. The point of no hand shock also happens to coincide somewhat with the node of vibration in many cases.
An impact can be modeled by a big force \(\mathbf{F}\) applied at point \(\mathbf{P}\) during a very small period of time \(\Delta t\). The variations of the speed of the centre of gravity \(\Delta \mathbf{V_G}\) and of the speed of rotation \(\Delta \mathbf{\Omega}\) answer to Newton’s laws:
\(
\displaystyle
\left\{
\begin{align}
\displaystyle
M \Delta \mathbf{V_G} =& \mathbf{F}\Delta t \\
M K \Delta \mathbf{\Omega} =& \mathbf{GP} \times \mathbf{F}\Delta t
\end{align}
\right.
\)
where \(M\) is the mass of the solid, and \(M K\) is the moment of inertia around \(\mathbf{G}\) (here I assume a planar motion with \(\mathbf{\Omega}\) vertical along \(\mathbf{z}\)).
Now let us write the variation of speed at another point \(\mathbf{Q}\):
\(
\displaystyle
\mathbf{V_Q} = \mathbf{V_G} + \mathbf{\Omega} \times \mathbf{GQ}
\)
\(
\displaystyle
\Delta\mathbf{V_Q} = \Delta\mathbf{V_G} + \Delta\mathbf{\Omega} \times \mathbf{GQ} + \mathbf{\Omega} \times \Delta\mathbf{GQ}
\)
We can safely neglect the last term, considering that the impact is very brief so that the points move very little during that time. Using the equations of motion written earlier:
\(
\displaystyle
M K \Delta\mathbf{V_Q} = K \mathbf{F}\Delta t + \left(\mathbf{GP} \times \mathbf{F}\Delta t \right) \times \mathbf{GQ}
\)
Let us see if we can find point \(\mathbf{Q}\) such that \(\Delta\mathbf{V_Q} = 0\). This gives:
\(
\begin{align}
\displaystyle
0 =& K \mathbf{F} + \left(\mathbf{GP} \times \mathbf{F} \right) \times \mathbf{GQ} \\
0 =& K \mathbf{F} + (\mathbf{GP} \cdot \mathbf{GQ})\; \mathbf{F} – (\mathbf{GQ} \cdot \mathbf{F})\; \mathbf{GP} \\
0 =& (K + \mathbf{GP} \cdot \mathbf{GQ})\; \mathbf{F} – (\mathbf{GQ} \cdot \mathbf{F})\; \mathbf{GP} \\
\end{align}
\)
Here two cases need to be distinguished. If \(\mathbf{F}\) and \(\mathbf{GP}\) are parallel, i.e. \(\mathbf{F}\) is pushing through \(\mathbf{G}\), there is no solution and all points see a variation of their speed. If they are not, then we need to have:
\(
\left\{
\begin{align}
\displaystyle
K + \mathbf{GP} \cdot \mathbf{GQ}\; =& 0 \\
\mathbf{GQ} \cdot \mathbf{F}\; =& 0
\end{align}
\right.
\)
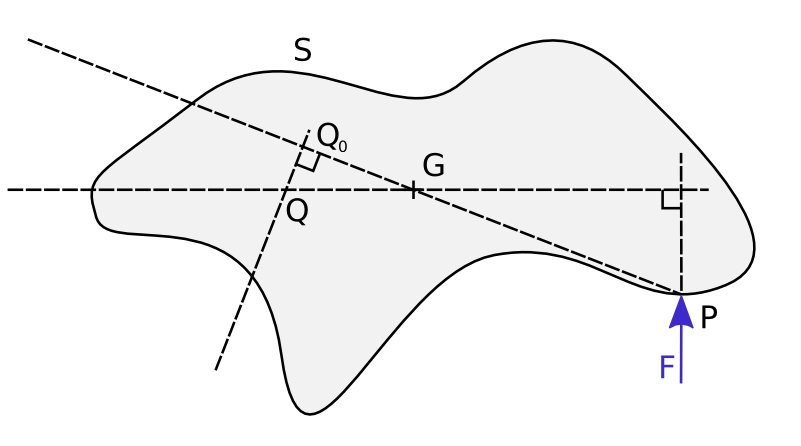
This happens to define exactly one point as shown on the figure below, at the intersection of two lines, one perpendicular to \(\mathbf{F}\) going through \(\mathbf{G}\), and the other perpendicular to \(GP\) and passing through point \(\mathbf{Q_0}\) such that \(\mathbf{GQ_0} = -\frac{K}{\mathbf{GP}^2}\mathbf{GP}\). That last property makes the link with the centre of percussion, as \(\mathbf{Q_0}\) is the centre of percussion associated to \(\mathbf{P}\).
For long objects such as swords the coincidence is even more obvious, as \(\mathbf{F}\) will nearly always be perpendicular to \(\mathbf{GP}\), such that \(\mathbf{Q}= \mathbf{Q_0}\). Point \(\mathbf{Q}\) has no name that I know of in physics; I would propose the name centre of acceleration associated to impact at \(\mathbf{P}\), as the object accelerates in rotation around that point.
The notion of centre of percussion finally appeared in specialised fencing books, for example Captain Del Frate Istruzione per maneggio e scherma della sciabola (1868, in Italian centro di percossa) as well as A New System of Sword Exercise for Infantry by Richard F. Burton in 1876. Although he is often cited on this topic, Burton seems to have taken most of his knowledge of the topic from Wilkinson and Latham. Use of the term subsisted into the 20th century, but with knowledge of swords being less and less relevant its meaning became less and less clear, hence the modern confusion in my opinion.
Conclusion
To conclude, here is a brief timeline of the history of the term:
- 5th century B.C.
- Formulation of the first questions about impact in general in the European culture
- 1621
- The problem of where to hit with the sword is considered by Baldi
- 1646
- First use of ‘centre of percussion’ by Mersenne and Fabri, identification with the centre of oscillation
- 1673
- A general solution to the problem is found by Huygens, applied to horology
- 1750s
- The term found its way into military dictionaries
- 1834
- Application to swords
- 1840s
- Appearance in military manuals
- Around 1844
- Beginnings of the confusion with the node of vibration
I hope this will help nuance the conclusions of George Turner’s article. Although there is a clear, universal physical meaning to ‘centre of percussion’, until relatively late it was a research topic, and not really meant for applications to swords. How it applies to swords exactly is also not so easy to model, and this is what confused the notion in that specific field during the 19th century.
In my opinion, the greatest significance of the notions of centre of percussion and centre of oscillation is not performance in cutting, but the understanding of handling properties. They embed knowledge about how the sword behave in rotation, and are irreplaceable for that. They give access to physical properties that are impossible to measure in static experiments. Using a sword never requires that level of theoretical understanding, which is why they remained absent from the technical literature for so long.

Very nice! You dug into more historical sources more than I did. ^_^
It’s all quite fascinating, isn’t it. In studying the history of pendular motion I did run across one odd reference to a drawing Leonardo Da Vinci made that had stumped people. It seemed to be some kind of pendulum device for measuring something, but nobody could figure out what it was for. Unfortunately, I couldn’t find an image of it, but it’s out there somewhere.
In my paper I also screwed up in suggesting a parabolic mass distribution (as a starting point) with the image of a parabola where m(x)=k*sqrt(x), instead of m(x)=k*x^2, which would be a pyramidal blade that would better describe a typical point. The ending of my no-math paper was kind of rushed due to the excitement being expressed as it was nearing completion.
Anyway, last week I was writing some code to find the balance point and moment of inertia of a blade whose mass distribution was m(x)=k*x^y, and while checking my equations ran across a reference to Archimedes determining the balance point of a parabola by comparing it to a triangle, and I thought “hmm…”
Hi George, great to have you here! I really want to thank you for setting me off in these studies…
It would be nice to see that Da Vinci drawing, although a pendulum device could be used for many things other than measuring centres of percussion. It’s quite possible that there was a pre-existent empirical knowledge on that topic though, especially from people using hammers for example. I have just not found the evidence yet. I figure you can’t build a durable water-powered trip hammer without taking the centre of percussion into account, and these predate the scientific studies I have described by hundreds of years…
And yes there is other stuff that I find disputable in your article, but I’m leaving that for later 🙂 My own work is not beyond reproach either, not by a long shot, but this is how knowledge advances, right? We need other people to take what we start and run with it a bit further!
Indeed we do, and I don’t read Latin, Italian, or French, which makes the source material problematic at best. ^_^
This book on the history of science goes on at length on the sword problem and what it led to. I’d swear it had page 500 included in the review when I first pulled it up, but continuing on.
Also of note in the next paragraph is that Descartes wrote a fighting manual and wasn’t impressed with Thibault!
Great stuff. Someone needs to buy that book.
At one point I was so deep into researching the problem that I actually contemplated paying $20,000 for an original copy of Wallis “De Motu.” Thank goodness sanity prevailed. Shortly after my short version was posted, Peter Johnsson took a bunch of measurements and found that often the center of percussion was a bit behind the tip. So there went that. ^_^
As I side note, I started my research based on an offhand conversation between John Clements and Hank Reinhardt at a sword conference. John was taking some flack for his early idea that maybe the cross guard was used to protect the knuckles when punching a shield, and they were perplexed that we still don’t know what the cross was for. That bugged me, because if the people who have read just about everything written about swords by later authors don’t know, then perhaps nobody knows. A typical sword has four parts. How could we not know what one of them is for?
Later, when browsing through a big book of arms and armor of the world, I noticed that there wasn’t a single example of a straight, double-edged sword that didn’t have quillons of some sort, even if they were positioned on the pommel, or used some other means of throwing a lot of mass offline from the blade, whereas on curved swords “hand protection” was completely optional. Viking swords probably had the least, but as I understand it their grips are quite flat.
So while welding a beefier tang on a big Del Tin hand-and-a-half sword, and making a bigger cross for no particular reason, I took advantage of its disassembled condition to try and use it without any quillons at all. It felt the same and swung the same, but was useless for combat because when struck with a rapier the blade would spin around, probably in about a millisecond or less. With a bare-handed death grip I could withstand medium rapier hits, but with gloves, blade alignment was impossible to control. With two or three hits the rapier man could even walk my blade around in circles till I was in the thumb grip, without me be able to stop him. So I clamped a couple of vice-grips to the blade and the problem magically went away. Riddle solved. The cross is always there because it has to be, and often looks like a barbel because that’s a smarter way to fix the problem.
So then I wondered, “What’s the pommel for?” That took a whole lot more work.
Currently I’m looking at making a cheap, do-it-yourself 3-D surface profiler that everybody could use to make extremely accurate measurements of museum pieces, including the hilt and pommel. I’ve got an old vertical screw-thread linear position stage, driven by a stepper motor, and if I mounted one of the now common hardware store laser levels on it, I could create a horizontal reference plane that could be moved up and down in very fine increments. If that shined on a sword that was held with its edge at an angle to a table (so the fuller wouldn’t be shadowed), you could position some digital cameras above it, take pictures, and process them to find the red contour line for each vertical increment of the laser level, thus easily making a complete 3-D model of the entire sword.
Since the sword is entirely steel except for the grip, you could compute the volume and mass distribution, and if you laid it across a pair of digital scales to get the exact balance point, you could compute the unseen tang/grip weight to good accuracy, especially if cross checked with the moment of inertia (perhaps taken with a torsion balance).
I you folks who live where all the museums are located took a lot of data like that, the number of things we’d learn would be tremendous, such as mass/stiffness distributions, how tightly the center of percussion was located on different types of swords, or from different regions, at different times, and other relationships we probably haven’t even suspected.
And of course then we could program our CNC machines and blade shapers to spit out exact copies of our favorites. 🙂
This is an excellent piece of scholarship! I have also noticed the name of John Wallis coming up in the references to the history of “center of percussion” ( Ernst Mach, The Science of Mechanics, p. 417, and Peter Krehl, History of Shockwaves). Wallis was a contemporary of Huygens. Unfortunately, I have not found the relevant portions of Wallis’s work online.
Thanks Ben! I have no doubt further details about the period researches could be dug up, I’ve come across references to Wallis too but nothing really detailed… I wonder if it wasn’t in the letters of René Descartes?